Class 6 Mathematics Chapter 01 Koshe Dekhi 1.3 Question Answer
ষষ্ঠ শ্রেণীর গণিতের প্রথম অধ্যায় “পূর্বপাঠের পুনরালোচনা” শিক্ষার্থীদের জন্য গুরুত্বপূর্ণ। এর “কষে দেখি ১.৩” অংশে ঐকিক নিয়ম গাণিতিক ক্রিয়ার অনুশীলন রয়েছে। এই অংশ শিক্ষার্থীদের আগের শ্রেণির ধারণাগুলো পুনরায় ঝালিয়ে নিতে সাহায্য করে। ধাপে ধাপে সমাধানের মাধ্যমে তারা সহজে বুঝতে পারে কিভাবে সমস্যার সমাধান করতে হয়। এই অনুশীলনগুলো যুক্তি ও বিশ্লেষণ ক্ষমতা বাড়ায় এবং ভবিষ্যতের গণিত অধ্যয়নের ভিত্তি শক্ত করে। এই ব্লগে আমরা “কষে দেখি ১.৩”-এর সব প্রশ্নের সহজ, স্পষ্ট ও ব্যাখ্যাসহ সমাধান তুলে ধরেছি যাতে শিক্ষার্থীরা সহজে শিখতে পারে।
1. ফাকা ঘরে লিখি
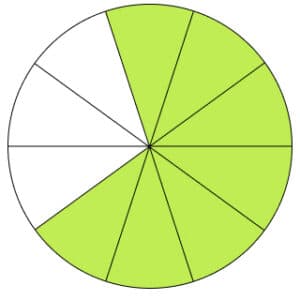
\dfrac{7}{10} অংশ রঙ করা।
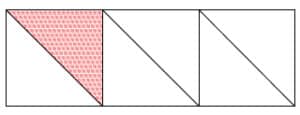
\dfrac{5}{6} অংশ রঙ করা নেই।

\dfrac{2}{5} অংশ রঙ করি। (ওপরের ছবিতে দেখানো হয়েছে )
2. মনে মনে ভেবে নিজে করি
(a) অর্ধেক রুটি বলতে মোট রুটির কত অংশ বোঝায়?
অর্ধেক রুটি মানে পুরো রুটির অর্ধাংশ।
অর্থাৎ,
\dfrac{1}{2} অংশ রুটি।
অতএব, অর্ধেক রুটি বলতে মোট রুটির \frac{1}{2} অংশ বোঝায়।
(b) আমার কাছে একটি বড়ো চকোলেট আছে। আমি সেই চকোলেটকে সমান 8টি টুকরো করে তার 3টি টুকরো বোনকে, 2টি টুকরো ভাইকে দিলাম ও বাকি টুকরোগুলি নিজে খেলাম। আমরা কে কে চকোলেটের কত অংশ পেলাম দেখাও।
চকোলেটটি 8টি টুকরো করা হয়েছে, তবে —
বোন পেয়েছে \dfrac{3}{8}, ভাই পেয়েছে \dfrac{2}{8},
অতএব, নিজে খেলাম \dfrac{3}{8} অংশ।

(c) 1 থেকে 10 পর্যন্ত পূর্ণসংখ্যাগুলি ও মৌলিক সংখ্যাগুলি লিখি। এদের মধ্যে মোট পূর্ণ সংখ্যার কত অংশ মৌলিক সংখ্যা আছে খুঁজে বের করো।
উত্তরঃ
1 থেকে 10 পর্যন্ত পূর্ণ সংখ্যা হলো —
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
এই সংখ্যাগুলির মধ্যে মৌলিক সংখ্যা হলো —
2, 3, 5, 7
অতএব, মৌলিক সংখ্যা মোট 4টি।
মোট পূর্ণ সংখ্যা = 10টি
অতএব, মৌলিক সংখ্যার ভগ্নাংশ = \dfrac{4}{10}
অর্থাৎ,
মৌলিক সংখ্যা পূর্ণ সংখ্যার \dfrac{4}{10} = \dfrac{2}{5} অংশ।
অতএব, মোট পূর্ণ সংখ্যার \dfrac{2}{5} অংশ হলো মৌলিক সংখ্যা।
(d) ঝুড়িতে কিছু কমলালেবু আছে। অর্ধেক লেবু দাদুকে দেওয়ার পরে ঝুড়িতে 2টি লেবু পড়ে রইল। দাদুকে দেওয়ার আগে ঝুড়িতে কত লেবু ছিল হিসাব করো।
উত্তরঃ
ধরি, ঝুড়িতে মোট লেবু ছিল xটি।
অর্ধেক লেবু দাদুকে দেওয়া হয়েছে, অর্থাৎ দাদু পেয়েছেন \dfrac{x}{2}টি লেবু।
বাকি লেবু আছে ২টি।
অতএব,
\dfrac{x}{2} = x - 2
এখন, সমীকরণটি সমাধান করি —
x - \dfrac{x}{2} = 2
\dfrac{x}{2} = 2
অতএব,
x = 4
অতএব, দাদুকে দেওয়ার আগে ঝুড়িতে মোট 4টি লেবু ছিল।
(e) একই মাপের দুটি গ্লাসে একই পরিমাণ সরবত তৈরি করা হলো। প্রথম গ্লাসের সরবতের \dfrac{1}{5} অংশ চিনি আছে, দ্বিতীয় গ্লাসের সরবতে \dfrac{2}{7} অংশ চিনি আছে। সরবত খাওয়ার আগেই কোন গ্লাসের সরবত বেশি মিষ্টি দেখাও।
উত্তরঃ
প্রথম গ্লাসে চিনির পরিমাণ = \dfrac{1}{5}
দ্বিতীয় গ্লাসে চিনির পরিমাণ = \dfrac{2}{7}
এখন দুই ভগ্নাংশকে তুলনা করার জন্য সমান হর করি —
\frac{1}{5} = \frac{7}{35} \Rightarrow \frac{2}{7} = \frac{10}{35}কারণ \frac{10}{35} > \frac{7}{35},
অতএব, দ্বিতীয় গ্লাসে চিনির পরিমাণ বেশি।
অতএব, দ্বিতীয় গ্লাসের সরবত বেশি মিষ্টি।
(f) স্কুলের গেটের \dfrac{5}{7} অংশ রং করা হয়ে গেছে। কত অংশ রং করতে এখনও বাকি আছে হিসাব করো।
উত্তরঃ
পুরো গেটকে 1 অংশ ধরা যাক।
রং করা হয়েছে \dfrac{5}{7} অংশ।
অতএব, বাকি রং করা বাকি অংশ = 1 - \dfrac{5}{7}
= \dfrac{7}{7} - \dfrac{5}{7} = \dfrac{2}{7}অতএব, গেটের \dfrac{2}{7} অংশ রং করা এখনও বাকি আছে।
(g) আমার কাছে 20 টাকা আছে। আমি 5 টাকা খরচ করলাম। আমি আমার টাকার কত অংশ খরচ করলাম ও কত অংশ এখনো আমার কাছে আছে হিসাব করো।
উত্তরঃ
মোট টাকা = 20 টাকা
খরচ হয়েছে = 5 টাকা
অতএব,
খরচ করা টাকার ভগ্নাংশ = \dfrac{5}{20} = \dfrac{1}{4}
এখন,
বাকি টাকার ভগ্নাংশ = 1 - \dfrac{1}{4} = \dfrac{3}{4}
অতএব,
আমি আমার টাকার \dfrac{1}{4} অংশ খরচ করেছি
ও \dfrac{3}{4} অংশ এখনো আমার কাছে আছে।
(h) রাজিয়ার কাছে 36টি কুল আছে। সে তার মোট কুলের \dfrac{1}{3} অংশ আমাকে দেবে। রাজিয়া কতগুলি কুল আমাকে দেবে হিসাব করো।
উত্তরঃ
রাজিয়ার মোট কুল = 36টি
দেওয়া হবে = মোট কুলের \dfrac{1}{3} অংশ
অতএব,
আমাকে দেওয়া কুলের সংখ্যা = \dfrac{1}{3} \times 36 = 12
অতএব, রাজিয়া আমাকে 12টি কুল দেবে।
3. ভগ্নাংশগুলি ছবির সাহায্যে দেখায়
(a) \dfrac{1}{5}

(b) \dfrac{3}{8}

(c) \dfrac{14}{5}
\dfrac{14}{5} = 2 \dfrac{4}{5}

এখানে 5 ভাগে ভাগ করা একটি ঘরকে পূর্ণ ধরে মোট ১৪টি অংশ কতটি পূর্ণ ঘর হয় তা বোঝানো হয়েছে।
✅ 14 ভাগকে 5 দিয়ে ভাগ করলে প্রথমে ২টি পূর্ণ ঘর পাওয়া যায় (কারণ 5×2 = 10)
✅ বাকি থাকে 4টি অংশ (14 – 10 = 4), যা তৃতীয় ঘরের 5 ভাগের মধ্যে 4 ভাগ রঙ করে দেখানো হয়েছে।
(d) 2 \dfrac{3}{7}

(e) \dfrac{8}{5}
\dfrac{8}{5} = 1 \dfrac{3}{5}

(f) \dfrac{11}{7}
\dfrac{11}{7} = 1 \dfrac{4}{7}

4. প্রকৃত ভগ্নাংশ, অপ্রকৃত ভগ্নাংশ ও মিশ্র ভগ্নাংশ গুলি আলাদা করে লিখি
\dfrac{1}{5},\dfrac{2}{7},\dfrac{3}{8},9\dfrac{14}{15},\dfrac{15}{13},\dfrac{6}{13},1\dfrac{22}{25},\dfrac{29}{19},\dfrac{1}{9},11\dfrac{1}{19},\dfrac{2}{5},\dfrac{5}{9},\dfrac{23}{17},2 \dfrac{3}{4},\dfrac{4}{17},3\dfrac{5}{11},\dfrac{11}{12},\dfrac{3}{7}
প্রকৃত ভগ্নাংশ (লব \lt হর): \dfrac{1}{5},\dfrac{2}{7},\dfrac{3}{8},\dfrac{6}{13},\dfrac{1}{9},\dfrac{2}{5},\dfrac{5}{9},\dfrac{4}{17},\dfrac{11}{12},\dfrac{3}{7}
অপ্রকৃত ভগ্নাংশ (লব ≥ হর কিন্তু মিশ্র নয়): \dfrac{15}{13},\dfrac{29}{19},\dfrac{23}{17}
মিশ্র ভগ্নাংশ (পূর্ণ সংখ্যা + ভগ্নাংশ): 9\dfrac{14}{15},1\dfrac{22}{25},11\dfrac{1}{19},2\dfrac{3}{4},3\dfrac{5}{11}
5. নিচের প্রতিটি ভগ্নাংশের তিনটি সমতুল্য ভগ্নাংশ লিখিঃ
(a) \dfrac{1}{5} এর তিনটি সমতুল্য ভগ্নাংশ লিখি —
উত্তরঃ
\dfrac{1}{5} এর সমতুল্য ভগ্নাংশগুলো হলো — \dfrac{2}{10}, \dfrac{3}{15}, \dfrac{4}{20}
(b) \dfrac{2}{5} এর তিনটি সমতুল্য ভগ্নাংশ লিখি —
উত্তরঃ
\dfrac{2}{5} এর সমতুল্য ভগ্নাংশগুলো হলো — \dfrac{4}{10}, \dfrac{6}{15}, \dfrac{8}{20}
(c) 1\dfrac{1}{3} এর তিনটি সমতুল্য ভগ্নাংশ লিখি —
উত্তরঃ
প্রথমে অপরিমিত ভগ্নাংশে রূপান্তর করি — 1\dfrac{1}{3} = \dfrac{4}{3}
এখন, \dfrac{4}{3} এর সমতুল্য ভগ্নাংশগুলো হলো — \dfrac{8}{6}, \dfrac{12}{9}, \dfrac{16}{12}
অতএব, 1\dfrac{1}{3} এর তিনটি সমতুল্য ভগ্নাংশ হলো — \dfrac{8}{6}, \dfrac{12}{9}, \dfrac{16}{12}।
(d) 6\dfrac{1}{6} এর তিনটি সমতুল্য ভগ্নাংশ লিখি —
প্রথমে অপরিমিত ভগ্নাংশে রূপান্তর করি —
6\dfrac{1}{6} = \dfrac{37}{6}
এখন, \dfrac{37}{6} এর সমতুল্য ভগ্নাংশগুলো হলো — \dfrac{74}{12}, \dfrac{111}{18}, \dfrac{148}{24}
অতএব, 6\dfrac{1}{6} এর তিনটি সমতুল্য ভগ্নাংশ হলো — \dfrac{74}{12}, \dfrac{111}{18}, \dfrac{148}{24}
(e) 3\dfrac{4}{5} এর তিনটি সমতুল্য ভগ্নাংশ লিখি —
উত্তরঃ
প্রথমে অপরিমিত ভগ্নাংশে রূপান্তর করি —
3\dfrac{4}{5} = \dfrac{19}{5}
এখন, \dfrac{19}{5} এর সমতুল্য ভগ্নাংশগুলো হলো — \dfrac{38}{10}, \dfrac{57}{15}, \dfrac{76}{20}
অতএব, 3\dfrac{4}{5} এর তিনটি সমতুল্য ভগ্নাংশ হলো — \dfrac{38}{10}, \dfrac{57}{15}, \dfrac{76}{20}
6. নিচের ভগ্নাংশগুলি কে লঘিষ্ঠ আকারে প্রকাশ করিঃ
(a) \dfrac{28}{49} ভগ্নাংশটিকে লঘিষ্ট আকারে প্রকাশ করি —
\dfrac{28}{49} এর লব ও হর উভয়কেই ৭ দিয়ে ভাগ করি — \dfrac{28 \div 7}{49 \div 7} = \dfrac{4}{7}
অতএব, \dfrac{28}{49} এর লঘিষ্ট আকার হলো \dfrac{4}{7}
(b) \dfrac{54}{81} ভগ্নাংশটিকে লঘিষ্ট আকারে প্রকাশ করি —
উত্তরঃ
\dfrac{54}{81} এর লব ও হর উভয়কেই ২৭ দিয়ে ভাগ করি —
অতএব, \dfrac{54}{81} এর লঘিষ্ট আকার হলো \dfrac{2}{3}।
(c) \dfrac{72}{108} ভগ্নাংশটিকে লঘিষ্ট আকারে প্রকাশ করি —
উত্তরঃ
\dfrac{72}{108} এর লব ও হর উভয়কেই ৩৬ দিয়ে ভাগ করি —
অতএব, \dfrac{72}{108} এর লঘিষ্ট আকার হলো \dfrac{2}{3}।
(d) \dfrac{243}{405} ভগ্নাংশটিকে লঘিষ্ট আকারে প্রকাশ করি —
উত্তরঃ
\dfrac{243}{405} এর লব ও হর উভয়কেই ৮১ দিয়ে ভাগ করি —
অতএব, \dfrac{243}{405} এর লঘিষ্ট আকার হলো \dfrac{3}{5}।
(e) \dfrac{165}{180} ভগ্নাংশটিকে লঘিষ্ট আকারে প্রকাশ করি —
উত্তরঃ
\dfrac{165}{180} এর লব ও হর উভয়কেই ১৫ দিয়ে ভাগ করি —
অতএব, \dfrac{165}{180} এর লঘিষ্ট আকার হলো \dfrac{11}{12}।
7. নিচের ভগ্নাংশগুলি কে ছোটো থেকে বড় (উর্ধক্রমে) সাজায়ঃ
(a) \dfrac{7}{2}, \dfrac{7}{4}, \dfrac{7}{5} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
প্রথমে তিনটি ভগ্নাংশকে সমান হরে আনতে হবে।
হরগুলো হলো 2, 4, ও 5
এদের ল.সা.গু = 20
এখন,
\dfrac{7}{2} = \dfrac{70}{20}, \dfrac{7}{4} = \dfrac{35}{20}, \dfrac{7}{5} = \dfrac{28}{20}
অতএব, ছোটো থেকে বড়ো ক্রমে —
\dfrac{7}{5}, \dfrac{7}{4}, \dfrac{7}{2}
(b) 5\dfrac{3}{4}, 5\dfrac{5}{9}, 5\dfrac{8}{12} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
প্রথমে মিশ্র ভগ্নাংশগুলোকে অপরিমিত ভগ্নাংশে বদলাই —
5\dfrac{3}{4} = \dfrac{23}{4}
5\dfrac{5}{9} = \dfrac{50}{9}
5\dfrac{8}{12} = \dfrac{68}{12}
এখন ভগ্নাংশগুলোকে তুলনা করার জন্য আমরা সবার হর (denominator) এক করি।
ভগ্নাংশগুলো ছিল —
\dfrac{23}{4},\ \dfrac{50}{9},\ \dfrac{68}{12}
এদের হর 4, 9 এবং 12 — তাই এই তিনটির ল.সা.গু (LCM) = 36
এখন প্রতিটি ভগ্নাংশকে 36 হর বিশিষ্ট ভগ্নাংশে রূপান্তর করি —
\dfrac{23}{4} = \dfrac{23 \times 9}{4 \times 9} = \dfrac{207}{36}
\dfrac{50}{9} = \dfrac{50 \times 4}{9 \times 4} = \dfrac{200}{36}
\dfrac{68}{12} = \dfrac{68 \times 3}{12 \times 3} = \dfrac{204}{36}
এখন তিনটি ভগ্নাংশের হর সমান, তাই শুধু লব (numerator) তুলনা করলেই যথেষ্ট —
200 \lt 204 \lt 207অতএব,
\dfrac{50}{9} \lt \dfrac{68}{12} \lt \dfrac{23}{4}অর্থাৎ মূল ভগ্নাংশগুলোর তুলনা —
5\dfrac{5}{9} \lt 5\dfrac{8}{12} \lt 5\dfrac{3}{4}সুতরাং, ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজালে পাই —
5\dfrac{5}{9},\ 5\dfrac{8}{12},\ 5\dfrac{3}{4}(c) 1\dfrac{1}{5}, 1\dfrac{1}{7}, 1\dfrac{1}{8} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
সবগুলো ভগ্নাংশের পূর্ণ সংখ্যা অংশ একই — 1
তাই শুধু ভগ্নাংশ অংশগুলিকে তুলনা করলেই হবে —
ভগ্নাংশ অংশগুলো হলো —
\dfrac{1}{5},\ \dfrac{1}{7},\ \dfrac{1}{8}
এখন তুলনা করার জন্য হরগুলো (5, 7, 8) এর ল.সা.গু (LCM) = 280
এগুলোকে 280 হর বিশিষ্ট ভগ্নাংশে রূপান্তর করি —
\dfrac{1}{5} = \dfrac{1 \times 56}{5 \times 56} = \dfrac{56}{280}
\dfrac{1}{7} = \dfrac{1 \times 40}{7 \times 40} = \dfrac{40}{280}
\dfrac{1}{8} = \dfrac{1 \times 35}{8 \times 35} = \dfrac{35}{280}
এখন হর সবার একই, তাই শুধু লব তুলনা করলে পাই —
35 \lt 40 \lt 56অতএব,
\dfrac{1}{8} \lt \dfrac{1}{7} \lt \dfrac{1}{5}এখন এগুলোকে মিশ্র ভগ্নাংশে লিখলে —
1\dfrac{1}{8} \lt 1\dfrac{1}{7} \lt 1\dfrac{1}{5}সুতরাং, ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজালে পাই —
1\dfrac{1}{8},\ 1\dfrac{1}{7},\ 1\dfrac{1}{5}(d) \dfrac{1}{3}, \dfrac{4}{5}, \dfrac{7}{15} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
হরগুলো হলো 3, 5 ও 15
এদের ল.সা.গু (LCM) = 15
এখন সব ভগ্নাংশকে 15 হর বিশিষ্ট ভগ্নাংশে রূপান্তর করি —
\dfrac{1}{3} = \dfrac{1 \times 5}{3 \times 5} = \dfrac{5}{15}
\dfrac{4}{5} = \dfrac{4 \times 3}{5 \times 3} = \dfrac{12}{15}
\dfrac{7}{15} = \dfrac{7}{15} (হর ইতিমধ্যেই 15)
এখন তিনটি ভগ্নাংশের হর সমান, তাই শুধু লব তুলনা করলেই হবে —
5 \lt 7 \lt 12অতএব,
\dfrac{5}{15} \lt \dfrac{7}{15} \lt \dfrac{12}{15}মূল ভগ্নাংশ অনুযায়ী —
\dfrac{1}{3} \lt \dfrac{7}{15} \lt \dfrac{4}{5}সুতরাং, ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজালে পাই —
\dfrac{1}{3},\ \dfrac{7}{15},\ \dfrac{4}{5}(e) \dfrac{5}{7}, \dfrac{3}{4}, \dfrac{1}{4} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
হরগুলো হলো 7 ও 4
এদের ল.সা.গু (LCM) = 28
এখন সব ভগ্নাংশকে 28 হর বিশিষ্ট ভগ্নাংশে রূপান্তর করি —
\dfrac{5}{7} = \dfrac{20}{28},
\dfrac{3}{4} = \dfrac{21}{28},
\dfrac{1}{4} = \dfrac{7}{28}
এখন তুলনা করলে দেখা যায় —
\dfrac{7}{28} \lt \dfrac{20}{28} \lt \dfrac{21}{28}অতএব, ছোটো থেকে বড়ো ক্রমে —
\dfrac{1}{4},\ \dfrac{5}{7},\ \dfrac{3}{4}(f) 3\dfrac{1}{2}, 7\dfrac{5}{9}, 7\dfrac{1}{5} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
প্রথমে মিশ্র ভগ্নাংশগুলোকে অপরিমিত ভগ্নাংশে রূপান্তর করি —
3\dfrac{1}{2} = \dfrac{7}{2},
7\dfrac{5}{9} = \dfrac{68}{9},
7\dfrac{1}{5} = \dfrac{36}{5}
এখন পূর্ণ সংখ্যা অংশ অনুযায়ী দেখা যায় —
3\dfrac{1}{2} এর মান 3-এর বেশি,
7\dfrac{1}{5} ও 7\dfrac{5}{9} — 7-এর বেশি।
অতএব, ছোটো থেকে বড়ো ক্রমে —
3\dfrac{1}{2},\ 7\dfrac{1}{5},\ 7\dfrac{5}{9}(g) \dfrac{1}{8}, \dfrac{7}{10}, \dfrac{3}{5} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
হরগুলো হলো 8, 10 ও 5
এদের ল.সা.গু (LCM) = 40
এখন সব ভগ্নাংশকে 40 হর বিশিষ্ট ভগ্নাংশে রূপান্তর করি —
\dfrac{1}{8} = \dfrac{5}{40},
\dfrac{7}{10} = \dfrac{28}{40},
\dfrac{3}{5} = \dfrac{24}{40}
এখন তুলনা করলে দেখা যায় —
\dfrac{5}{40} \lt \dfrac{24}{40} \lt \dfrac{28}{40}অতএব, ছোটো থেকে বড়ো ক্রমে —
\dfrac{1}{8},\ \dfrac{3}{5},\ \dfrac{7}{10}(h) 3\dfrac{1}{2}, 3\dfrac{5}{9}, 3\dfrac{1}{5} ভগ্নাংশগুলিকে ছোটো থেকে বড়ো (উর্ধ্বক্রমে) সাজাই —
উত্তরঃ
সবগুলোর পূর্ণ সংখ্যা অংশ একই (3),
তাই ভগ্নাংশ অংশগুলিকে তুলনা করলেই হবে —
\dfrac{1}{2},\ \dfrac{5}{9},\ \dfrac{1}{5}
এখন তুলনা করলে দেখা যায় —
\dfrac{1}{5} \lt \dfrac{5}{9} \lt \dfrac{1}{2}
অতএব, ছোটো থেকে বড়ো ক্রমে —
3\dfrac{1}{5},\ 3\dfrac{5}{9},\ 3\dfrac{1}{2}8. মান বের করিঃ
(a) \dfrac{2}{7} + \dfrac{2}{3} + 1\dfrac{1}{2} এর মান নির্ণয় করো —
উত্তরঃ
প্রথমে 1\dfrac{1}{2} = \dfrac{3}{2}
এখন,
\dfrac{2}{7} + \dfrac{2}{3} + \dfrac{3}{2}
হরগুলির ল.সা.গু = 42
অতএব,
\dfrac{2}{7} = \dfrac{12}{42}, \quad \dfrac{2}{3} = \dfrac{28}{42}, \quad \dfrac{3}{2} = \dfrac{63}{42}
এখন যোগ করি —
\dfrac{12 + 28 + 63}{42} = \dfrac{103}{42}
অতএব,
\dfrac{103}{42} = 2\dfrac{19}{42}
উত্তরঃ 2\dfrac{19}{42}
(b) 1\dfrac{2}{5} - \dfrac{3}{8} + \dfrac{1}{4} এর মান নির্ণয় করো —
উত্তরঃ
প্রথমে 1\dfrac{2}{5} = \dfrac{7}{5}
এখন,
\dfrac{7}{5} - \dfrac{3}{8} + \dfrac{1}{4}
হরগুলির ল.সা.গু = 40
অতএব,
\dfrac{7}{5} = \dfrac{56}{40}, \quad \dfrac{3}{8} = \dfrac{15}{40}, \quad \dfrac{1}{4} = \dfrac{10}{40}
এখন,
\dfrac{56}{40} - \dfrac{15}{40} + \dfrac{10}{40} = \dfrac{56 - 15 + 10}{40} = \dfrac{51}{40}
অতএব,
\dfrac{51}{40} = 1\dfrac{11}{40}
উত্তরঃ 1\dfrac{11}{40}
(c) \dfrac{2}{5} + \dfrac{3}{8} - \dfrac{1}{4} এর মান নির্ণয় করো —
উত্তরঃ
প্রথমে হরগুলির ল.সা.গু = 40
অতএব,
\dfrac{2}{5} = \dfrac{16}{40}, \quad \dfrac{3}{8} = \dfrac{15}{40}, \quad \dfrac{1}{4} = \dfrac{10}{40}
এখন,
\dfrac{16}{40} + \dfrac{15}{40} - \dfrac{10}{40} = \dfrac{21}{40}
অতএব,
উত্তরঃ \dfrac{21}{40}
(d) 7 - 3\dfrac{1}{8} - 2\dfrac{1}{3} এর মান নির্ণয় করো —
প্রথমে মিশ্র ভগ্নাংশগুলোকে অপরিমিত ভগ্নাংশে রূপান্তর করি —
3\dfrac{1}{8} = \dfrac{25}{8},
2\dfrac{1}{3} = \dfrac{7}{3}
এখন,
7 - \dfrac{25}{8} - \dfrac{7}{3}
হরগুলির ল.সা.গু = 24
অতএব,
7 = \dfrac{168}{24}, \quad \dfrac{25}{8} = \dfrac{75}{24}, \quad \dfrac{7}{3} = \dfrac{56}{24}
এখন,
\dfrac{168 - 75 - 56}{24} = \dfrac{37}{24}
অতএব,
\dfrac{37}{24} = 1\dfrac{13}{24}
উত্তরঃ 1\dfrac{13}{24}
(e) \dfrac{4}{5} + \dfrac{5}{8} - 1\dfrac{1}{3} এর মান নির্ণয় করো —
প্রথমে 1\dfrac{1}{3} = \dfrac{4}{3}
এখন,
\dfrac{4}{5} + \dfrac{5}{8} - \dfrac{4}{3}
হরগুলির ল.সা.গু = 120
অতএব,
\dfrac{4}{5} = \dfrac{96}{120}, \quad \dfrac{5}{8} = \dfrac{75}{120}, \quad \dfrac{4}{3} = \dfrac{160}{120}
এখন,
\dfrac{96 + 75 - 160}{120} = \dfrac{11}{120}
অতএব,
উত্তরঃ \dfrac{11}{120}
(f) 3\dfrac{1}{2} + 1\dfrac{1}{3} - 1\dfrac{1}{4} এর মান নির্ণয় করো —
প্রথমে মিশ্র ভগ্নাংশগুলোকে অপরিমিত ভগ্নাংশে রূপান্তর করি —
3\dfrac{1}{2} = \dfrac{7}{2},
1\dfrac{1}{3} = \dfrac{4}{3},
1\dfrac{1}{4} = \dfrac{5}{4}
এখন,
\dfrac{7}{2} + \dfrac{4}{3} - \dfrac{5}{4}
হরগুলির ল.সা.গু = 12
অতএব,
\dfrac{7}{2} = \dfrac{42}{12}, \quad \dfrac{4}{3} = \dfrac{16}{12}, \quad \dfrac{5}{4} = \dfrac{15}{12}
এখন,
\dfrac{42 + 16 - 15}{12} = \dfrac{43}{12}
অতএব,
\dfrac{43}{12} = 3\dfrac{7}{12}
উত্তরঃ 3\dfrac{7}{12}
(g) 1\dfrac{2}{3} + \dfrac{3}{5} - \dfrac{3}{10} এর মান নির্ণয় করো —
প্রথমে 1\dfrac{2}{3} = \dfrac{5}{3}
এখন,
\dfrac{5}{3} + \dfrac{3}{5} - \dfrac{3}{10}
হরগুলির ল.সা.গু = 30
অতএব,
\dfrac{5}{3} = \dfrac{50}{30}, \quad \dfrac{3}{5} = \dfrac{18}{30}, \quad \dfrac{3}{10} = \dfrac{9}{30}
এখন,
\dfrac{50 + 18 - 9}{30} = \dfrac{59}{30}
অতএব,
\dfrac{59}{30} = 1\dfrac{29}{30}
উত্তরঃ 1\dfrac{29}{30}
(h) 5\dfrac{2}{3} - 2\dfrac{3}{5} + 1\dfrac{1}{2} এর মান নির্ণয় করো —
প্রথমে মিশ্র ভগ্নাংশগুলোকে অপরিমিত ভগ্নাংশে রূপান্তর করি —
5\dfrac{2}{3} = \dfrac{17}{3},
2\dfrac{3}{5} = \dfrac{13}{5},
1\dfrac{1}{2} = \dfrac{3}{2}
এখন,
\dfrac{17}{3} - \dfrac{13}{5} + \dfrac{3}{2}
হরগুলির ল.সা.গু = 30
অতএব,
\dfrac{17}{3} = \dfrac{170}{30}, \quad \dfrac{13}{5} = \dfrac{78}{30}, \quad \dfrac{3}{2} = \dfrac{45}{30}
এখন,
\dfrac{170 - 78 + 45}{30} = \dfrac{137}{30}
অতএব,
\dfrac{137}{30} = 4\dfrac{17}{30}
উত্তরঃ 4\dfrac{17}{30}
9. হিসেব করিঃ
(a) \dfrac{2}{3}-এর সঙ্গে কত যোগ করলে 2 পাওয়া যায়?
উত্তরঃ
ধরি, যোগ করতে হবে x
অতএব,
\dfrac{2}{3} + x = 2
এখন,
x = 2 - \dfrac{2}{3}
= \dfrac{6}{3} - \dfrac{2}{3}
= \dfrac{4}{3}
অতএব, \dfrac{2}{3}-এর সঙ্গে \dfrac{4}{3} যোগ করলে 2 পাওয়া যায়।
অর্থাৎ, যোগ করতে হবে \dfrac{4}{3} বা 1\dfrac{1}{3}।
(b) আজ টিফিনের সময়ে স্কুলের সম্পূর্ণ ভর্তি জলের ট্যাঙ্কের \dfrac{1}{4} অংশ জল খরচ হয়েছে। ছুটির সময়ে দেখা গেল আরও \dfrac{1}{3} অংশ জল খরচ হয়েছে। ছুটির পরে ট্যাঙ্কে কত অংশ জল পড়ে আছে দেখাও।
উত্তরঃ
ধরি, পুরো ট্যাঙ্কে মোট জল = 1 অংশ।
টিফিনের সময়ে খরচ হয়েছে \dfrac{1}{4} অংশ,
ছুটির সময়ে আরও খরচ হয়েছে \dfrac{1}{3} অংশ।
অতএব, মোট খরচ হয়েছে = \dfrac{1}{4} + \dfrac{1}{3}
হরগুলির ল.সা.গু = 12
অতএব,
\dfrac{1}{4} = \dfrac{3}{12}, \quad \dfrac{1}{3} = \dfrac{4}{12}
এখন,
\dfrac{3}{12} + \dfrac{4}{12} = \dfrac{7}{12}
অতএব, খরচ হয়েছে \dfrac{7}{12} অংশ জল।
বাকি জল = 1 - \dfrac{7}{12} = \dfrac{12}{12} - \dfrac{7}{12} = \dfrac{5}{12}
অতএব, ছুটির পরে ট্যাঙ্কে \dfrac{5}{12} অংশ জল পড়ে আছে।
(c) আজ টিফিনে আমি কেক নিয়ে গিয়েছিলাম। আমার দুই বন্ধু আয়ুষ ও সাবানা আমার কেকের যথাক্রমে \dfrac{1}{3} অংশ ও \dfrac{2}{5} অংশ খেল। কেকের বাকি অংশটা আমি খেলাম। কে বেশি কেক খেল হিসাব করো।
উত্তরঃ
ধরি, পুরো কেক = 1 অংশ।
আয়ুষ খেয়েছে \dfrac{1}{3} অংশ,
সাবানা খেয়েছে \dfrac{2}{5} অংশ।
অতএব, দু’জন মোট খেয়েছে = \dfrac{1}{3} + \dfrac{2}{5}
হরগুলির ল.সা.গু = 15
অতএব,
\dfrac{1}{3} = \dfrac{5}{15}, \quad \dfrac{2}{5} = \dfrac{6}{15}
এখন,
\dfrac{5}{15} + \dfrac{6}{15} = \dfrac{11}{15}
অতএব, দু’জন মিলে খেয়েছে \dfrac{11}{15} অংশ কেক।
বাকি কেক আমি খেয়েছি = 1 - \dfrac{11}{15} = \dfrac{15}{15} - \dfrac{11}{15} = \dfrac{4}{15}
এখন,
আয়ুষ খেয়েছে \dfrac{1}{3} = \dfrac{5}{15},
সাবানা খেয়েছে \dfrac{2}{5} = \dfrac{6}{15},
আমি খেয়েছি \dfrac{4}{15}।
অতএব, সাবানা সবচেয়ে বেশি কেক খেয়েছে।
(d) রতনবাবু তাঁর ২৫ বিঘা জমির মধ্যে ১৬ বিঘা জমিতে পাট চাষ করেছেন। কিন্তু ঊষাদেবী তাঁর ১৫ বিঘা জমির মধ্যে ৮ বিঘা জমিতে পাট চাষ করেছেন। হিসাব করে দেখো রতনবাবু ও ঊষাদেবী তাঁদের জমির কত অংশে পাট চাষ করেছেন ও কে বেশি পরিমাণ জমিতে পাট চাষ করেছেন।
উত্তরঃ
রতনবাবুর পাট চাষের অংশ = \dfrac{16}{25}
ঊষাদেবীর পাট চাষের অংশ = \dfrac{8}{15}
এখন, দুই ভগ্নাংশের তুলনা করার জন্য সমান হর করি —
হরগুলির ল.সা.গু = 75
অতএব,
\dfrac{16}{25} = \dfrac{48}{75},
\dfrac{8}{15} = \dfrac{40}{75}
এখন দেখা যাচ্ছে —
\dfrac{48}{75} > \dfrac{40}{75}
অতএব, রতনবাবু তাঁর জমির তুলনায় বেশি অংশে পাট চাষ করেছেন।
(e) আমার ১৫ মিটার লম্বা সাদা ফিতে আছে। আমি \dfrac{1}{3} অংশ কেটে নিলাম। কত অংশ সাদা ফিতে পড়ে রইল ও সেটি কতটা লম্বা বের করি।
উত্তরঃ
মোট ফিতে = ১ অংশ = ১৫ মিটার
কাটা হয়েছে \dfrac{1}{3} অংশ
অতএব, বাকি অংশ = 1 - \dfrac{1}{3} = \dfrac{2}{3}
অতএব, সাদা ফিতের \dfrac{2}{3} অংশ পড়ে রইল।
এখন, বাকি ফিতের দৈর্ঘ্য = \dfrac{2}{3} \times 15
= 10 মিটার
অতএব, সাদা ফিতের \dfrac{2}{3} অংশ অর্থাৎ ১০ মিটার ফিতে পড়ে রইল।
আমাদের লক্ষ্য সবসময় শিক্ষার্থীদের জন্য সঠিক ও নির্ভুল তথ্য প্রদান করা। তবুও অনিচ্ছাকৃতভাবে কোনো ভুল হয়ে গেলে, আমরা চাই সেটি যেন দ্রুত সংশোধন করা হয়।
যদি উপরের পোস্টটিতে কোনো ভুল বা অসঙ্গতি খুঁজে পান, অনুগ্রহ করে মন্তব্যে জানাবেন। আপনার সহযোগিতা আমাদের জন্য অমূল্য — কারণ আমরা চাই না কোনো শিক্ষার্থী ভুল শিখুক।
মনে রাখবেন: আপনার দেওয়া ছোট্ট একটি মন্তব্য অনেকের শেখার পথ সঠিক রাখতে সাহায্য করবে।