Madhyamik 2026 Mathematics Question Paper Solution
মাধ্যামিক ২০২৬ পরীক্ষার্থীদের জন্য গণিত প্রশ্নপত্রের সম্পূর্ণ সমাধান এখানে দেওয়া হলো। এই পোস্টে বহুবিকল্পধর্মী প্রশ্ন, সংক্ষিপ্ত অঙ্ক, ধাপে ধাপে গাণিতিক সমাধান এবং পূর্ণমানের প্রশ্নের উত্তর সহজ বাংলা ব্যাখ্যাসহ উপস্থাপন করা হয়েছে। অধ্যায়ভিত্তিক ও প্রশ্নভিত্তিক এই সমাধান শিক্ষার্থীদের পরীক্ষার প্রস্তুতিকে আরও শক্তিশালী ও আত্মবিশ্বাসী করে তুলবে।
1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচনকরঃ
i. কোন মূলধন 10 বছরে দ্বিগুণ হলে, বার্ষিক সরল সুদের হার কত হবে?
সরল সুদের ক্ষেত্রে,
অর্থ 10 বছরে দ্বিগুণ হলে সুদের পরিমাণ = আসল।
সূত্র অনুযায়ী,
সুদ = (মূলধন × হার × সময়) / 100
যেহেতু সুদ = মূলধন,
⇒ (P × R × 10) / 100 = P
⇒ R × 10 = 100
⇒ R = 10
অতএব বার্ষিক সরল সুদের হার = 10%
ii. ax^2 + bx + c = 0 \ (a \gt 0) এর বীজ দুটি সমান কিন্তু বিপরীত চিহ্নযুক্ত হওয়ার শর্ত কোনটি?
দুটি বীজ সমান হলে,
b^2 - 4ac = 0
এবং দুটি বীজ বিপরীত চিহ্নযুক্ত হলে,
\frac{c}{a} \lt 0
যেহেতু a \gt 0,
সুতরাং c \lt 0 হতে হবে।
আবার বীজ দুটি সমান হওয়ার জন্য,
b = 0
অতএব শর্ত হবে:
b = 0, \ c \lt 0
সঠিক উত্তর: b = 0, \ c \lt 0
iii. 6, 7, x, y, 16 সংখ্যাগুলির গড় 9 হলে নিচের কোনটি সঠিক?
গড় = (সব সংখ্যার যোগফল) ÷ (সংখ্যার সংখ্যা)
সুতরাং,
\frac{6 + 7 + x + y + 16}{5} = 9
⇒ 6 + 7 + 16 + x + y = 45
⇒ 29 + x + y = 45
⇒ x + y = 45 - 29
⇒ x + y = 16
সঠিক উত্তর: x + y = 16
iv. একটি বৃত্তের 121 সেমি দৈর্ঘ্যের চাপ কেন্দ্রে 77° কোণ উৎপন্ন করলে বৃত্তটির ব্যাসার্ধ কত হবে?
চাপের দৈর্ঘ্যের সূত্র:
চাপ = (θ / 360) × 2πr
সুতরাং,
121 = \frac{77}{360} \times 2 \times \frac{22}{7} \times r
⇒ 121 = \frac{77 \times 2 \times 22}{360 \times 7} \times r
এখানে 77 ÷ 7 = 11 এবং 121 ÷ 11 = 11
⇒ 11 = \frac{2 \times 22}{360} \times r
⇒ 11 = \frac{44}{360} \times r
⇒ 1 = \frac{4}{360} \times r
⇒ r = \frac{360}{4}
⇒ r = 90
অতএব বৃত্তটির ব্যাসার্ধ = 90 সেমি
সঠিক উত্তর: 90 সেমি
v. একটি ঘনকের একটি বাহুর দৈর্ঘ্য a একক এবং কর্ণের দৈর্ঘ্য d একক হলে a ও d এর সম্পর্ক হবে—
ধরা যাক ঘনকের একটি বাহুর দৈর্ঘ্য = a
ঘনকের কর্ণের সূত্র অনুযায়ী,
d = \sqrt{a^2 + a^2 + a^2}
⇒ d = \sqrt{3a^2}
⇒ d = \sqrt{3}\,a
অতএব a ও d এর সম্পর্ক হলো:
\sqrt{3}\,a = d
সঠিক উত্তর: \sqrt{3}\,a = d
6. O কেন্দ্রবিশিষ্ট বৃত্তের ABCD একটি বৃত্তীয় চতুর্ভুজ। BC কে E পর্যন্ত বর্ধিত করা হলো। যদি ∠DCE = 96° হয়, তবে ∠BOD এর মান কত?
প্রশ্নে অসঙ্গতি রয়েছে
2. শূন্যস্থান পূরণ করো (যে কোন পাঁচটি):
(i) এক বছরে আসল ও সুদ-আসলের অনুপাত 8 : 9 হলে বার্ষিক সুদের হার __________
তবে সুদ-আসল = 9x
সুদ = 9x − 8x = x
হার = (সুদ ÷ আসল) × 100
= (x ÷ 8x) × 100
= 12.5%
সঠিক উত্তর: 12.5%
(ii) (√3 − 5) এর অনুবন্ধী কর্ণী নির্ণয় করো।
কোনো মিশ্র কর্ণীর অনুবন্ধী কর্ণী পেতে হলে কর্ণীর অমূলদ অংশের (যে অংশের সাথে √ আছে) চিহ্ন পরিবর্তন করতে হয়, কিন্তু মূলদ অংশ অপরিবর্তিত থাকে।
এখানে কর্ণীটি হলো: √3 − 5
অমূলদ অংশ = √3
মূলদ অংশ = −5
অতএব, √3 এর চিহ্ন পরিবর্তন করলে পাই −√3
এবং −5 অপরিবর্তিত থাকবে।
সুতরাং,
(√3 − 5) এর অনুবন্ধী কর্ণী = −√3 − 5
অথবা, −(√3 + 5)
যাচাই:
যোগফল: (√3 − 5) + (−√3 − 5) = −10 (মূলদ সংখ্যা)
গুণফল: (√3 − 5)(−√3 − 5) = −(3 − 25) = 22 (মূলদ সংখ্যা)
সঠিক উত্তর: −√3 − 5
(iii) কোনো বৃত্তের একটি ব্যাসের দুই প্রান্তে অঙ্কিত স্পর্শকদ্বয় পরস্পর __________
(iv) যদি x = a \sec \theta এবং y = b \cot \theta হয়, তবে \left(\frac{x^2}{a^2} - \frac{b^2}{y^2}\right) এর মান নির্ণয় করো।
দেওয়া আছে,
x = a \sec \theta \Rightarrow \frac{x^2}{a^2} = \sec^2 \theta
এবং,
y = b \cot \theta \Rightarrow \frac{b^2}{y^2} = \tan^2 \theta
অতএব,
\frac{x^2}{a^2} - \frac{b^2}{y^2} = \sec^2 \theta - \tan^2 \theta
আমরা জানি,
\sec^2 \theta - \tan^2 \theta = 1
সঠিক উত্তর: 1
(v) একটি নিরেট অর্ধগোলকের ব্যাসার্ধ 3r হলে, তার সমগ্র তলের ক্ষেত্রফল কত?
3\pi r^2
এখানে ব্যাসার্ধ,
r = 3r
সুতরাং,
\text{সমগ্র তলের ক্ষেত্রফল} = 3\pi (3r)^2
= 3\pi \times 9r^2
= 27\pi r^2
সঠিক উত্তর: 27\pi r^2
3. সত্য বা মিথ্যা লেখো (যে কোন পাঁচটি):
(i) \sin^2 \theta = (\sin \theta)^2,\; 0^\circ \lt; \theta \lt; 90^\circ
ব্যাখ্যা: সংজ্ঞা অনুযায়ী,
\sin^2 \theta অর্থই হলো (\sin \theta)^2।
সুতরাং উক্তিটি সত্য।
(ii) 4 সেমি ব্যাসার্ধ বিশিষ্ট গোলকের মধ্যে অন্তর্লিখিত বৃহত্তম ঘনকের বাহুর দৈর্ঘ্য 4\sqrt{2} সেমি।
ব্যাখ্যা:
যদি একটি ঘনক কোনো গোলকের মধ্যে অন্তর্লিখিত হয়, তবে ঘনকের সর্ববৃহৎ কর্ণ (Space Diagonal) গোলকের ব্যাসের সমান হয়।
ধরা যাক,
ঘনকের বাহু = a
তবে ঘনকের কর্ণ = a\sqrt{3}
গোলকের ব্যাসার্ধ r = 4 সেমি
⇒ গোলকের ব্যাস = 2r = 8 সেমি
অতএব,
a\sqrt{3} = 8
⇒ a = \frac{8}{\sqrt{3}} সেমি
কিন্তু প্রশ্নে বাহুর দৈর্ঘ্য 4\sqrt{2} সেমি বলা হয়েছে, যা সঠিক নয়।
সঠিক উত্তর: মিথ্যা
(iii) অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থিত কোণ স্থূলকোণ।
ব্যাখ্যা: জ্যামিতির উপপাদ্য অনুযায়ী—
অর্ধবৃত্তস্থ কোণ = 90° (সমকোণ)।
অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থিত কোণ \lt 90° (সূক্ষ্মকোণ)।
অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থিত কোণ \gt 90° (স্থূলকোণ)।
যেহেতু অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থিত কোণ সূক্ষ্মকোণ হয়, তাই প্রশ্নে প্রদত্ত উক্তিটি মিথ্যা।
সঠিক উত্তর: মিথ্যা
(iv) x-3, x-1, 7, x, 2x-1, 3x-5 রাশিগুলির যৌগিক গড় 7.5 হলে উহাদের মধ্যমা 3 হবে।
ব্যাখ্যা:
1. প্রথমে গড় থেকে x এর মান নির্ণয় করি—
\frac{(x-3)+(x-1)+7+x+(2x-1)+(3x-5)}{6}=7.5
⇒ \frac{8x-3}{6}=7.5
⇒ 8x-3=45
⇒ 8x=48
⇒ x=6
2. রাশিগুলি হবে—
3, 5, 7, 6, 11, 13
3. ঊর্ধ্বক্রমে সাজালে পাই—
3, 5, 6, 7, 11, 13
4. মধ্যমা—
\frac{6+7}{2}=6.5
যেহেতু মধ্যমা 6.5, কিন্তু প্রশ্নে 3 বলা হয়েছে, তাই বিবৃতিটি মিথ্যা।
সঠিক উত্তর: মিথ্যা
(v) যদি x \propto \frac{1}{y} হয়, তবে (xy)^{10} ধ্রুবক।
ব্যাখ্যা:
1. দেওয়া আছে,
x \propto \frac{1}{y}
⇒ x = \frac{k}{y}, যেখানে k একটি অশূন্য ভেদ ধ্রুবক।
⇒ xy = k
2. উভয় পক্ষকে 10 ঘাতে উন্নীত করলে পাই—
(xy)^{10} = k^{10}
যেহেতু k একটি ধ্রুবক, তাই k^{10} ও ধ্রুবক।
অতএব, (xy)^{10} একটি ধ্রুবক।
সঠিক উত্তর: সত্য
(vi) একটি ব্যবসায় রাজু ও আসিফের মূলধনের অনুপাত 5:4 এবং রাজু মোট লাভের 80 টাকা পেলে আসিফ পায় 100 টাকা।
ব্যাখ্যা:
1. আমরা জানি, লাভ মূলধনের অনুপাতে বণ্টিত হয়।
অতএব,
\text{রাজুর লাভ} : \text{আসিফের লাভ} = 5 : 4
2. দেওয়া আছে,
\text{রাজুর লাভ} = 80 টাকা।
ধরি, আসিফের লাভ = a টাকা।
3. শর্ত অনুযায়ী,
\frac{80}{a} = \frac{5}{4}
⇒ 5a = 320
⇒ a = 64 টাকা।
কিন্তু প্রশ্নে আসিফের লাভ 100 টাকা বলা হয়েছে, যা সঠিক নয়।
অতএব, বিবৃতিটি মিথ্যা।
সঠিক উত্তর: মিথ্যা
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাও (যে কোন দশটি):
(i) A এবং B যথাক্রমে 15,000 টাকা ও 45,000 টাকা দিয়ে একটি ব্যবসা শুরু করে। 6 মাস পরে B তার লাভের হিসাবে 3,030 টাকা পেলে, A এর লাভাংশ কত?
A ও B একই সময় (6 মাস) ব্যবসা করেছে।
অতএব লাভের অনুপাত = মূলধনের অনুপাত
A : B = 15000 : 45000 = 1 : 3
ধরা যাক,
A এর লাভ = x টাকা
তবে B এর লাভ = 3x টাকা
প্রশ্ন অনুযায়ী,
3x = 3030
অতএব,
A এর লাভাংশ = 1010 টাকা।
(ii) ΔABC এর BC বাহুর সমান্তরাল একটি সরলরেখা AB ও AC কে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। যদি AP = 4 সেমি, QC = 9 সেমি এবং PB = AQ হয়, তবে PB এর মান নির্ণয় করো।
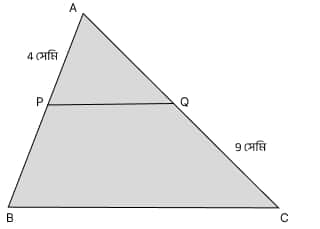
BC এর সমান্তরাল রেখা AB ও AC কে ছেদ করায় সমানুপাতিক বিভাজনের সূত্র প্রযোজ্য।
ধরা যাক,
PB = AQ = x সেমি
তবে,
AB = AP + PB = 4 + x
AC = AQ + QC = x + 9
সমানুপাতিক বিভাজন সূত্র অনুযায়ী,
\frac{AP}{AB} = \frac{AQ}{AC}
অতএব,
\frac{4}{4 + x} = \frac{x}{x + 9}
অতএব,
PB = 6 সেমি।
(iii) O কেন্দ্রবিশিষ্ট বৃত্তের AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী। যদি ∠AOB = 60° এবং CD = 6 সেমি হয়, তবে বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য কত?
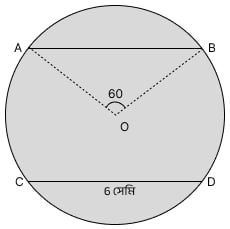
যেহেতু AB ও CD জ্যা দুটি কেন্দ্র থেকে সমদূরবর্তী,
অতএব জ্যা দুটির দৈর্ঘ্য সমান।
সুতরাং,
AB = CD = 6 সেমি
এখন ∠AOB = 60° হলে,
জ্যা AB এর দৈর্ঘ্যের সূত্র অনুযায়ী—
AB = 2r \sin \frac{\angle AOB}{2}
অতএব,
6 = 2r \sin 30^\circ
আমরা জানি,
\sin 30^\circ = \frac{1}{2}
সুতরাং,
6 = 2r \times \frac{1}{2}
\Rightarrow 6 = r
অতএব,
বৃত্তটির ব্যাসার্ধ = 6 সেমি।
(iv) যদি \tan \theta + \cot \theta = 2 হয়, তবে \tan^7 \theta + \cot^7 \theta এর মান নির্ণয় করো।
দেওয়া আছে,
\tan \theta + \cot \theta = 2
আমরা জানি,
\tan \theta + \cot \theta \ge 2
সমতা তখনই হবে যখন,
\tan \theta = \cot \theta = 1
অতএব,
\tan^7 \theta = 1^7 = 1
এবং
\cot^7 \theta = 1^7 = 1
সুতরাং,
\tan^7 \theta + \cot^7 \theta = 1 + 1 = 2
অতএব চাওয়া মান = 2।
(v) x ও y ধনাত্মক রাশি হলে, \sec \theta = \frac{x}{y} হতে পারে কি? উত্তরের সপক্ষে যুক্তি দাও।
আমরা জানি,
\sec \theta = \frac{1}{\cos \theta}
এবং বাস্তব কোণের জন্য,
\cos \theta \le 1
অতএব,
\sec \theta \ge 1
যেহেতু x ও y উভয়ই ধনাত্মক রাশি,
\frac{x}{y} \gt 0
কিন্তু \sec \theta = \frac{x}{y} হওয়ার জন্য শর্ত হলো—
\frac{x}{y} \ge 1, অর্থাৎ x \ge y
সুতরাং,
x \ge y হলে \sec \theta = \frac{x}{y} হতে পারে।
অতএব উত্তর: হ্যাঁ, হতে পারে।
(vi) দুটি লম্ববৃত্তাকার চোঙের উচ্চতার অনুপাত 1:2 এবং ভূমির পরিধির অনুপাত 3:4 হলে, তাদের আয়তনের অনুপাত নির্ণয় করো।
দেওয়া আছে:
1. উচ্চতার অনুপাত—
h_1 : h_2 = 1 : 2 \Rightarrow \frac{h_1}{h_2} = \frac{1}{2}
2. ভূমির পরিধির অনুপাত—
2\pi r_1 : 2\pi r_2 = 3 : 4 \Rightarrow \frac{r_1}{r_2} = \frac{3}{4}
আমরা জানি, লম্ববৃত্তাকার চোঙের আয়তনের সূত্র—
V = \frac{1}{3}\pi r^2 h
সুতরাং, চোঙ দুটির আয়তনের অনুপাত—
V_1 : V_2 = \pi r_1^2 h_1 : \pi r_2^2 h_2
অতএব, দুই চোঙের আয়তনের অনুপাত = 9 : 32।
সঠিক উত্তর: 9 : 32
(vii) যদি x_1, x_2, \dots, x_n রাশিগুলির গাণিতিক গড় \bar{x} হয়, তবে প্রমাণ কর যে,
\displaystyle \sum_{i=1}^{n}(x_i-\bar{x})^2 = \sum_{i=1}^{n}x_i^2-n\bar{x}^2।
দেওয়া আছে,
\displaystyle \bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_i
এখন,
\displaystyle
\sum_{i=1}^{n}(x_i-\bar{x})^2
= \displaystyle \sum_{i=1}^{n}(x_i^2-2x_i\bar{x}+\bar{x}^2)
= \displaystyle \sum_{i=1}^{n}x_i^2-2\bar{x}\sum_{i=1}^{n}x_i+\sum_{i=1}^{n}\bar{x}^2
যেহেতু
\displaystyle \sum_{i=1}^{n}x_i=n\bar{x} এবং
\displaystyle \sum_{i=1}^{n}\bar{x}^2=n\bar{x}^2,
অতএব,
\displaystyle
\sum_{i=1}^{n}(x_i-\bar{x})^2
=\sum_{i=1}^{n}x_i^2-2n\bar{x}^2+n\bar{x}^2
=\sum_{i=1}^{n}x_i^2-n\bar{x}^2
অতএব প্রমাণিত।
(viii) সুদের হার 5.5% থেকে 6%-এ বৃদ্ধি পেলে কিছু টাকার বার্ষিক সুদ 49.50 টাকা বৃদ্ধি পায়। আসল নির্ণয় করো।
সুদের হার বৃদ্ধি = 6\%-5.5\%=0.5\%
ধরা যাক, আসল = P টাকা।
বার্ষিক সুদের বৃদ্ধি,
\frac{0.5}{100}\times P=49.50
অতএব, আসল = 9900 টাকা।
(ix) x^2-4x=K(x-1)-5 সমীকরণটির বীজ দুটির সমষ্টি 7 হলে, K-এর মান নির্ণয় করো।
প্রদত্ত সমীকরণটি সাজাই—
x^2-4x=Kx-K-5 \Rightarrow x^2-(4+K)x+(K+5)=0
আমরা জানি, দ্বিঘাত সমীকরণ
ax^2+bx+c=0 হলে, বীজদ্বয়ের সমষ্টি
=-\frac{b}{a}
এখানে,
a=1,\; b=-(4+K)
অতএব বীজদ্বয়ের সমষ্টি
=4+K
প্রশ্ন অনুযায়ী,
4+K=7
অতএব, K-এর মান = 3।
(x) (a+b):\sqrt{ab}=2:1 হলে a:b নির্ণয় করো।
দেওয়া আছে,
\frac{a+b}{\sqrt{ab}}=2 \Rightarrow a+b=2\sqrt{ab}
উভয় পাশে বর্গ করি—
(a+b)^2=4ab
অতএব,
a:b=1:1।
(xi) একটি গোলকের ব্যাসার্ধ 50% বাড়ালে আয়তন শতকরা কত বাড়বে?
ধরা যাক, গোলকের প্রাথমিক ব্যাসার্ধ = r।
ব্যাসার্ধ 50% বাড়লে নতুন ব্যাসার্ধ
=1.5r।
আমরা জানি, গোলকের আয়তন
V \propto r^3।
অতএব আয়তনের অনুপাত,
\frac{V_2}{V_1}=\left(\frac{1.5r}{r}\right)^3=(1.5)^3=3.375।
আয়তন বৃদ্ধি
=(3.375-1)\times100\%=2.375\times100\%=237.5\%।
অতএব আয়তন বৃদ্ধি পাবে 237.5\%।
(xii) ABCD একটি বৃত্তীয় চতুর্ভুজ। যদি AD=AB, \angle DAC=60^\circ এবং \angle BDC=50^\circ হয়, তবে \angle ACD এর মান নির্ণয় করো।
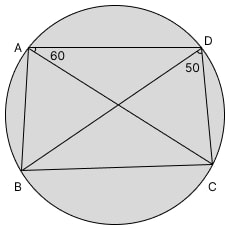
ধাপ ১: একই বৃত্তচাপের ওপর অবস্থিত কোণের ধারণা ব্যবহার
আমরা জানি, একই বৃত্তচাপের ওপর অবস্থিত সকল বৃত্তস্থ কোণ সমান।
বৃত্তচাপ BC-এর ওপর অবস্থিত কোণ
\angle BAC=\angle BDC=50^\circ।
সুতরাং,
\angle DAB=\angle DAC+\angle BAC=60^\circ+50^\circ=110^\circ।
ধাপ ২: সমদ্বিবাহু ত্রিভুজ \triangle ABD থেকে কোণ নির্ণয়
দেওয়া আছে, AB=AD।
অতএব \triangle ABD একটি সমদ্বিবাহু ত্রিভুজ এবং
\angle ABD=\angle ADB।
ত্রিভুজের কোণগুলির সমষ্টি,
\angle ABD+\angle ADB+\angle DAB=180^\circ
\Rightarrow 2\angle ADB+110^\circ=180^\circ
\Rightarrow 2\angle ADB=70^\circ
\Rightarrow \angle ADB=35^\circ
ধাপ ৩: চূড়ান্ত কোণ \angle ACD নির্ণয়
বৃত্তচাপ AD-এর ওপর অবস্থিত কোণদ্বয় হলো
\angle ABD এবং \angle ACD।
অতএব,
\angle ACD=\angle ABD।
আবার, সমদ্বিবাহু ত্রিভুজ থেকে
\angle ABD=\angle ADB=35^\circ।
সুতরাং,
\angle ACD=35^\circ।
সঠিক উত্তর: 35^\circ
5. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) যদি বার্ষিক চক্রবৃদ্ধি সুদের হার প্রথম বছরে 4\% ও দ্বিতীয় বছরে 5\% হয়, তবে 25{,}000 টাকার দুই বছরের সুদ নির্ণয় করো।
P=25{,}000 টাকা।
প্রথম বছরে পরিমাণ,
A_1=25{,}000\left(1+\frac{4}{100}\right)=25{,}000\times1.04=26{,}000
দ্বিতীয় বছরে পরিমাণ,
A_2=26{,}000\left(1+\frac{5}{100}\right)=26{,}000\times1.05=27{,}300
দুই বছরের মোট সুদ,
\text{সুদ}=27{,}300-25{,}000=2{,}300 টাকা।
অতএব, দুই বছরের সুদ = 2{,}300 টাকা।
(ii) তিন বন্ধু যথাক্রমে 4{,}800 টাকা, 6{,}600 টাকা ও 9{,}600 টাকা নিয়ে একটি যৌথ ব্যবসা শুরু করল। প্রথম জন দেখাশোনার জন্য লাভের \frac{1}{8} অংশ বেতন হিসেবে পেল এবং বাকি লাভ মূলধনের অনুপাতে বণ্টিত হল। এক বছর পরে প্রথম জন 780 টাকা পেলে বাকি দু’জন কত টাকা করে পাবে?
প্রথম জন বেতন হিসেবে পেল
\frac{x}{8}
অতএব বণ্টনযোগ্য লাভ
=x-\frac{x}{8}=\frac{7x}{8}
মূলধনের অনুপাত
4{,}800:6{,}600:9{,}600=24:33:48
অতএব প্রথম জনের অংশ
=\frac{24}{24+33+48}\times\frac{7x}{8}=\frac{24}{105}\times\frac{7x}{8}=\frac{x}{5}
প্রশ্ন অনুযায়ী,
\frac{x}{8}+\frac{x}{5}=780
\Rightarrow \frac{13x}{40}=780
\Rightarrow x=2400
অতএব বণ্টনযোগ্য লাভ
=\frac{7}{8}\times2400=2100
দ্বিতীয় জনের অংশ
=\frac{33}{105}\times2100=660 টাকা।
তৃতীয় জনের অংশ
=\frac{48}{105}\times2100=960 টাকা।
সুতরাং,
দ্বিতীয় জন পাবে 660 টাকা এবং তৃতীয় জন পাবে 960 টাকা।
6. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) সমাধান করো: b(c-a)x^2+c(a-b)x+a(b-c)=0
b(c-a)x^2+c(a-b)x+a(b-c)=0
সমস্ত পদের সহগের যোগফল, b(c-a)+c(a-b)+a(b-c)=0
অতএব, x=1 একটি মূল।
এখন দ্বিঘাত সমীকরণের সূত্র অনুযায়ী,
দুটি মূলের গুণফল
একটি মূল 1 হলে অপর মূল,
=\frac{a(b-c)}{b(c-a)}
অতএব সমীকরণের সমাধান,
x=1 অথবা x=\frac{a(b-c)}{b(c-a)}
(ii) দুই অঙ্কের একটি সংখ্যার দশকের অঙ্ক এককের অঙ্ক অপেক্ষা 3 কম। অঙ্কদ্বয়ের গুণফল সংখ্যা থেকে 15 কম। সংখ্যাটি নির্ণয় করো।
তবে দশকের অঙ্ক = x-3।
সংখ্যাটি হবে
10(x-3)+x=11x-30।
অঙ্কদ্বয়ের গুণফল
=x(x-3)=x^2-3x।
প্রশ্ন অনুযায়ী,
x^2-3x=(11x-30)-15
\Rightarrow x^2-3x=11x-45
\Rightarrow x^2-14x+45=0
অতএব,
x=5 \text{ অথবা } x=9।
দশকের অঙ্ক হবে যথাক্রমে
2 বা 6।
সুতরাং সংখ্যাগুলি হলো
25 \text{ ও } 69
7. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) যদি (x^3+y^3)\propto(x^3-y^3) হয়, তবে দেখাও যে (x^2+y^2)\propto xy।
দেওয়া আছে,
(x^3+y^3)\propto(x^3-y^3)
\Rightarrow \frac{x^3+y^3}{x^3-y^3}=k, যেখানে k একটি অশূন্য ধ্রুবক।
যোগ–ভাগ প্রক্রিয়া প্রয়োগ করে পাই,
\frac{(x^3+y^3)+(x^3-y^3)}{(x^3+y^3)-(x^3-y^3)}=\frac{k+1}{k-1}
\Rightarrow \frac{2x^3}{2y^3}=m, যেখানে m=\frac{k+1}{k-1} একটি ধ্রুবক।
\Rightarrow \frac{x^3}{y^3}=m
\Rightarrow \frac{x}{y}=\sqrt[3]{m}=n (ধ্রুবক)
\Rightarrow x=ny
এখন,
\frac{x^2+y^2}{xy}=\frac{(ny)^2+y^2}{(ny)y}
যেহেতু n একটি ধ্রুবক, তাই
\frac{x^2+y^2}{xy} ধ্রুবক।
অতএব,
(x^2+y^2)\propto xy (প্রমাণিত)।
(ii) যদি x(2-\sqrt{3})=y(2+\sqrt{3})=1 হয়, তবে 3x^2-5xy+3y^2 এর মান নির্ণয় করো।
দেওয়া আছে,
x(2-\sqrt{3})=1 \Rightarrow x=\frac{1}{2-\sqrt{3}}
y(2+\sqrt{3})=1 \Rightarrow y=\frac{1}{2+\sqrt{3}}
হরের করণী নিরসন করে পাই,
x=\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}=\frac{2+\sqrt{3}}{4-3}=2+\sqrt{3}
y=\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}=\frac{2-\sqrt{3}}{4-3}=2-\sqrt{3}
প্রয়োজনীয় মানসমূহ:
x+y=(2+\sqrt{3})+(2-\sqrt{3})=4
xy=(2+\sqrt{3})(2-\sqrt{3})=4-3=1
এখন প্রদত্ত রাশি:
3x^2-5xy+3y^2
=3(x^2+y^2)-5xy
=3\{(x+y)^2-2xy\}-5xy
=3(16-2)-5=42-5=37
সঠিক উত্তর: 37
8. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) যদি \frac{a+b-c}{a+b}=\frac{b+c-a}{b+c}=\frac{c+a-b}{c+a} এবং a+b+c\neq0 হয়, তবে প্রমাণ কর যে a=b=c
দেওয়া আছে,
\frac{a+b-c}{a+b}=\frac{b+c-a}{b+c}=\frac{c+a-b}{c+a}
সংযোজন প্রক্রিয়া (Addendo) প্রয়োগ করে পাই, প্রতিটি অনুপাত
=\frac{(a+b-c)+(b+c-a)+(c+a-b)}{(a+b)+(b+c)+(c+a)}
যেহেতু a+b+c\neq0,
অতএব প্রতিটি অনুপাত
=\frac{1}{2}
এখন প্রথম অনুপাত থেকে,
\frac{a+b-c}{a+b}=\frac{1}{2}
\Rightarrow 2a+2b-2c=a+b
\Rightarrow a+b=2c …(i)
দ্বিতীয় অনুপাত থেকে,
\frac{b+c-a}{b+c}=\frac{1}{2}
\Rightarrow 2b+2c-2a=b+c
\Rightarrow b+c=2a …(ii)
(i) থেকে b=2c-a বসিয়ে (ii)-এ পাই,
(2c-a)+c=2a
\Rightarrow 3c=3a
\Rightarrow a=c
অনুরূপভাবে প্রমাণ করা যায় যে,
a=b
অতএব,
a=b=c (প্রমাণিত)।
(ii) যদি x=\frac{8ab}{a+b} হয়, তবে
\frac{x+4a}{x-4a}+\frac{x+4b}{x-4b} এর মান নির্ণয় করো।
দেওয়া আছে,
x=\frac{8ab}{a+b}
প্রথম ভগ্নাংশটি বিবেচনা করি—
\frac{x+4a}{x-4a}=\frac{\frac{8ab}{a+b}+4a}{\frac{8ab}{a+b}-4a}
অনুরূপভাবে,
\frac{x+4b}{x-4b}=\frac{3a+b}{a-b}
অতএব প্রদত্ত রাশির মান,
\frac{a+3b}{b-a}+\frac{3a+b}{a-b}
অতএব, চাওয়া মান = 2
9. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) প্রমাণ কর যে, কোনো বৃত্তের একটি বৃত্তচাপ দ্বারা গঠিত কেন্দ্রীয় কোণ ঐ চাপের দ্বারা গঠিত বৃত্তস্থ কোণের দ্বিগুণ।
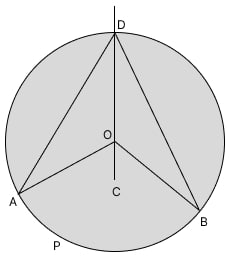
প্রমাণ:
চিত্র পরিচিতি:
ধরি, একটি বৃত্তের কেন্দ্র O। APB একটি বৃত্তচাপ, যার দ্বারা গঠিত কেন্দ্রস্থ কোণ \angle AOB এবং বৃত্তস্থ কোণ \angle ADB (বা \angle ACB)।
অঙ্কন:
D ও O যোগ করে সরলরেখাটি C বিন্দু পর্যন্ত বর্ধিত করি।
প্রমাণ:
\triangle AOD-এ,
OA = OD (একই বৃত্তের ব্যাসার্ধ)।
অতএব,
\angle OAD = \angle ODA।
আবার, \triangle AOD-এর বহিঃস্থ কোণ
\angle AOC = \angle OAD + \angle ODA
(ত্রিভুজের বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান)।
অতএব,
\angle AOC = 2\angle ODA …(i)
একইভাবে, \triangle BOD থেকে পাই,
\angle BOC = 2\angle ODB …(ii)
এখন (i) ও (ii) যোগ করলে,
\angle AOC + \angle BOC = 2(\angle ODA + \angle ODB)
অতএব,
\angle AOB = 2\angle ADB
সুতরাং, কেন্দ্রস্থ কোণ = 2 × বৃত্তস্থ কোণ। (প্রমাণিত)
(ii) প্রমাণ কর যে, দুটি বৃত্ত পরস্পরকে স্পর্শ করলে স্পর্শবিন্দুটি কেন্দ্র দুটির সংযোগক সরলরেখার উপর অবস্থিত হবে।
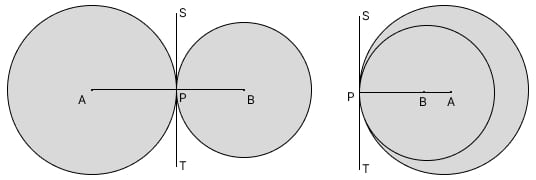
প্রমাণ:
চিত্র পরিচিতি:
ধরি, A ও B কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে P বিন্দুতে স্পর্শ করেছে।
প্রমাণ করতে হবে যে, A, P, B সমরেখ (অর্থাৎ একই সরলরেখায় অবস্থিত)।
অঙ্কন:
AP ও BP যোগ করা হলো।
প্রমাণ:
1. যেহেতু বৃত্ত দুটি P বিন্দুতে পরস্পরকে স্পর্শ করেছে, তাই P বিন্দুতে একটি সাধারণ স্পর্শক থাকবে। ধরি, ST হলো P বিন্দুতে সাধারণ স্পর্শক।
2. A কেন্দ্রবিশিষ্ট বৃত্তের ক্ষেত্রে, AP হলো স্পর্শবিন্দুগামী ব্যাসার্ধ এবং ST স্পর্শক।
আমরা জানি, স্পর্শবিন্দুগামী ব্যাসার্ধ স্পর্শকের উপর লম্ব।
অতএব,
AP \perp ST \Rightarrow \angle APT = 90^\circ।
3. একইভাবে, B কেন্দ্রবিশিষ্ট বৃত্তের ক্ষেত্রে,
BP \perp ST \Rightarrow \angle BPT = 90^\circ।
4. অতএব,
\angle APB = \angle APT + \angle BPT = 90^\circ + 90^\circ = 180^\circ।
যেহেতু \angle APB একটি সরলকোণ, তাই
A, P, B একই সরলরেখায় অবস্থিত।
অতএব প্রমাণিত যে, দুটি বৃত্ত পরস্পরকে স্পর্শ করলে স্পর্শবিন্দুটি কেন্দ্র দুটির সংযোগক সরলরেখার উপর অবস্থিত হবে।
10. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) একটি সমদ্বিবাহু ত্রিভুজ ABC-এর \angle B সমকোণ।
\angle BAC-এর সমদ্বিখণ্ডক BC-কে D বিন্দুতে ছেদ করেছে।
প্রমাণ কর যে, CD^2 = 2BD^2।
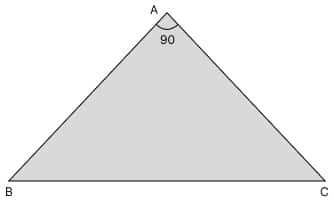
প্রদত্ত:
\triangle ABC-এর \angle B = 90^\circ এবং এটি একটি সমদ্বিবাহু ত্রিভুজ। যেহেতু অতিভুজ বৃহত্তম বাহু, তাই সমান বাহু দুটি হলো AB ও BC। অতএব, AB = BC।
ধাপ ১: পিথাগোরাসের উপপাদ্য প্রয়োগ
সমকোণী ত্রিভুজ ABC-এ,
AC^2 = AB^2 + BC^2
\Rightarrow AC^2 = AB^2 + AB^2 \quad (\text{যেহেতু } AB = BC)
\Rightarrow AC^2 = 2AB^2
\Rightarrow AC = \sqrt{2}\,AB …(i)
ধাপ ২: কোণ-সমদ্বিখণ্ডক উপপাদ্য প্রয়োগ
\angle BAC-এর সমদ্বিখণ্ডক AD, BC-কে D বিন্দুতে ছেদ করেছে।
উপপাদ্য অনুযায়ী,
\frac{BD}{DC}=\frac{AB}{AC}
ধাপ ৩: মান বসিয়ে প্রমাণ
(i) থেকে AC=\sqrt{2}\,AB বসালে পাই,
\frac{BD}{DC}=\frac{AB}{\sqrt{2}\,AB}=\frac{1}{\sqrt{2}}
উভয় পাশে বর্গ করলে,
DC^2=(\sqrt{2}\,BD)^2=2BD^2
অতএব,
CD^2 = 2BD^2 (প্রমাণিত)।
(ii) ABCD আয়তক্ষেত্রের অভ্যন্তরে O একটি বিন্দু। প্রমাণ কর যে,
OA^2 + OC^2 = OB^2 + OD^2।
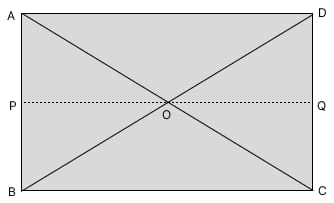
অঙ্কন:
O বিন্দুর মধ্য দিয়ে BC বাহুর সমান্তরাল একটি সরলরেখা অঙ্কন করলাম, যা AB বাহুকে P বিন্দুতে এবং DC বাহুকে Q বিন্দুতে ছেদ করে।
যেহেতু ABCD একটি আয়তক্ষেত্র এবং PQ \parallel BC, তাই
PQ \perp AB এবং PQ \perp DC।
অতএব, APQD এবং PBCQ উভয়ই আয়তক্ষেত্র।
সুতরাং,
AP = DQ \quad \text{এবং} \quad PB = QC।
ধাপ ১: বামপক্ষের মান নির্ণয়
সমকোণী ত্রিভুজ \triangle APO থেকে পিথাগোরাসের উপপাদ্য অনুযায়ী,
OA^2 = AP^2 + OP^2 …(i)
আবার, সমকোণী ত্রিভুজ \triangle OQC থেকে পাই,
OC^2 = OQ^2 + QC^2 …(ii)
(i) ও (ii) যোগ করলে,
OA^2 + OC^2 = AP^2 + OP^2 + OQ^2 + QC^2 …(iii)
ধাপ ২: ডানপক্ষের মান নির্ণয়
সমকোণী ত্রিভুজ \triangle OPB থেকে পাই,
OB^2 = OP^2 + PB^2 = OP^2 + QC^2
(যেহেতু PB = QC) …(iv)
সমকোণী ত্রিভুজ \triangle OQD থেকে পাই,
OD^2 = OQ^2 + DQ^2 = OQ^2 + AP^2
(যেহেতু DQ = AP) …(v)
(iv) ও (v) যোগ করলে,
OB^2 + OD^2 = OP^2 + QC^2 + OQ^2 + AP^2 …(vi)
(iii) এবং (vi) নং সমীকরণ তুলনা করে দেখা যায় যে উভয়ের ডানপক্ষ সমান।
অতএব, OA^2 + OC^2 = OB^2 + OD^2 (প্রমাণিত)।
11. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) \triangle ABC-এর ভূমি BC = 6 সেমি, \angle ABC = 60^\circ এবং AB = 8 সেমি। ঐ ত্রিভুজটির পরিবৃত্ত অঙ্কন করো।
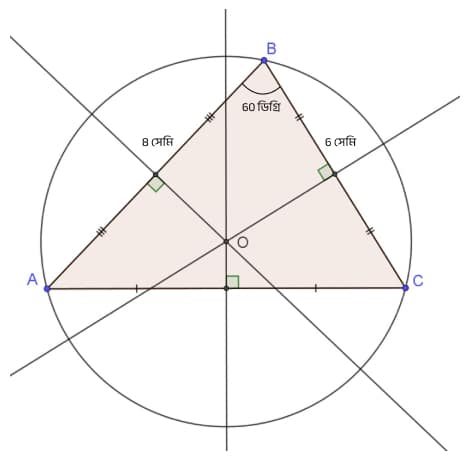
অঙ্কন পদ্ধতি:
1. প্রথমে একটি সরলরেখায় BC = 6 সেমি আঁকলাম।
2. B বিন্দুতে \angle ABC = 60^\circ কোণ অঙ্কন করলাম এবং সেই কোণের এক বাহু বরাবর BA = 8 সেমি চিহ্নিত করে A বিন্দু নিলাম।
3. A ও C যোগ করে \triangle ABC সম্পূর্ণ করলাম।
4. এখন AB বাহুর লম্বদ্বিখণ্ডক অঙ্কন করলাম।
5. অনুরূপভাবে BC বাহুর লম্বদ্বিখণ্ডক অঙ্কন করলাম।
6. এই দুই লম্বদ্বিখণ্ডক পরস্পরকে O বিন্দুতে ছেদ করল।
7. O বিন্দুকে কেন্দ্র এবং OA (বা OB, OC) ব্যাসার্ধ ধরে একটি বৃত্ত আঁকলাম।
এই বৃত্তটি A, B, C তিনটি বিন্দুর মধ্য দিয়ে অতিক্রম করে।
এটাই প্রয়োজনীয় পরিবৃত্ত।
(ii) 6 সেমি বাহু বিশিষ্ট একটি সমবাহু ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট একটি বর্গক্ষেত্র অঙ্কন করো।
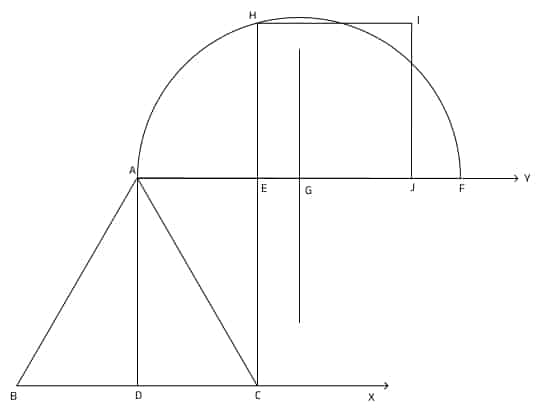
অঙ্কন পদ্ধতি:
1. প্রথমে একটি রশ্মি BX নিলাম এবং তাতে BC = 6 সেমি কেটে নিলাম।
2. B ও C বিন্দুকে কেন্দ্র করে 6 সেমি ব্যাসার্ধ নিয়ে উপরের দিকে দুটি বৃত্তচাপ অঙ্কন করলাম, যা পরস্পরকে A বিন্দুতে ছেদ করল।
AB ও AC যোগ করে সমবাহু ত্রিভুজ \triangle ABC অঙ্কন করলাম।
3. A বিন্দু দিয়ে ভূমি BC-এর সমান্তরাল একটি সরলরেখা AY অঙ্কন করলাম।
4. ভূমি BC-কে লম্বভাবে সমদ্বিখণ্ডিত করলাম। লম্বটি BC-কে D বিন্দুতে এবং সমান্তরাল রেখা AY-কে E বিন্দুতে ছেদ করল।
5. E বিন্দু থেকে AY রেখার উপর DC-এর সমান দৈর্ঘ্যের একটি অংশ EF কেটে নিলাম।
6. AF রেখাংশকে সমদ্বিখণ্ডিত করে মধ্যবিন্দু G নির্ণয় করলাম।
G বিন্দুকে কেন্দ্র করে GA ব্যাসার্ধ নিয়ে একটি অর্ধবৃত্ত অঙ্কন করলাম।
7. EC লম্বটিকে উপরের দিকে বর্ধিত করলাম, যা অর্ধবৃত্তকে H বিন্দুতে ছেদ করল।
এই EH হলো প্রয়োজনীয় বর্গক্ষেত্রের একটি বাহু।
8. EH বাহুকে ভিত্তি ধরে বর্গক্ষেত্র EHIJ সম্পন্ন করলাম।
সুতরাং, সমবাহু ত্রিভুজ ABC-এর সমান ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্র EHIJ অঙ্কিত হলো।
12. যে কোন দুটি প্রশ্নের উত্তর দাও:
(i) একটি ত্রিভুজের কোণ তিনটির অনুপাত 2:3:4 হলে ত্রিভুজটির বৃহত্তম কোণটির বৃত্তীয় মান নির্ণয় করো।
2x,\,3x,\,4x।
ত্রিভুজের তিন কোণের সমষ্টি
=180^\circ।
অতএব,
2x+3x+4x=180^\circ
\Rightarrow 9x=180^\circ
\Rightarrow x=20^\circ
বৃহত্তম কোণ
=4x=4\times20^\circ=80^\circ
এখন, বৃত্তীয় মান = ডিগ্রি মান × \frac{\pi}{180}
অতএব বৃহত্তম কোণের বৃত্তীয় মান
=80^\circ\times\frac{\pi}{180}=\frac{4\pi}{9}
সঠিক উত্তর: \frac{4\pi}{9}
(ii) যদি \tan\theta=\frac{4}{3} হয়, তবে \sin\theta+\cos\theta-এর মান নির্ণয় করো।
\tan\theta=\frac{4}{3}
ধরি, একটি সমকোণী ত্রিভুজে
লম্ব = 4 একক,
ভূমি = 3 একক।
তাহলে অতিভুজ
=\sqrt{4^2+3^2}=\sqrt{16+9}=5 একক।
অতএব,
\sin\theta=\frac{4}{5}
এবং
\cos\theta=\frac{3}{5}
সুতরাং,
\sin\theta+\cos\theta=\frac{4}{5}+\frac{3}{5}=\frac{7}{5}
সঠিক উত্তর: \frac{7}{5}
(iii) A ও B দুটি পরস্পর পূরক কোণ হলে প্রমাণ কর যে,
(\sin A+\cos B)^2=1+2\sin A\sin B।
13. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) একটি বাড়ির ছাদ থেকে একটি ল্যাম্পপোস্টের চূড়া ও পাদবিন্দুর অবনতি কোণ যথাক্রমে 30^\circ ও \theta^\circ।
বাড়ি ও ল্যাম্পপোস্টের উচ্চতার অনুপাত 3:2 হলে \theta-এর মান নির্ণয় করো।
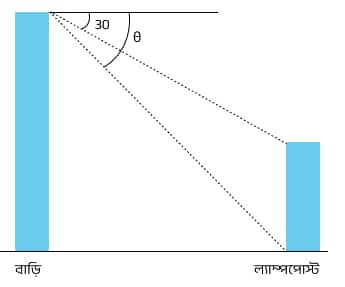
ধরি,
বাড়ির উচ্চতা = 3x
ল্যাম্পপোস্টের উচ্চতা = 2x
ধরি, বাড়ির পাদবিন্দু থেকে ল্যাম্পপোস্টের পাদবিন্দুর অনুভূমিক দূরত্ব = d।
চূড়ার জন্য:
অবনতি কোণ = 30^\circ
\tan 30^\circ=\frac{3x-2x}{d}=\frac{x}{d}
\Rightarrow \frac{1}{\sqrt{3}}=\frac{x}{d}
\Rightarrow d=\sqrt{3}x …(i)
পাদবিন্দুর জন্য:
অবনতি কোণ = \theta
(i) থেকে d=\sqrt{3}x বসিয়ে পাই,
\tan\theta=\frac{3x}{\sqrt{3}x}=\sqrt{3}
সঠিক উত্তর: \theta=60^\circ
(ii) একটি টিলার পাদদেশ থেকে তার শীর্ষের উন্নতি কোণ 45^\circ।
টিলার দিকে 30^\circ ঢাল বেয়ে 100 মিটার এগোনোর পর উন্নতি কোণ হয় 60^\circ।
টিলার উচ্চতা নির্ণয় করো।
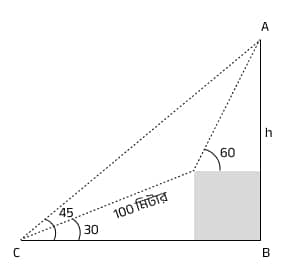
ধরি, টিলার উচ্চতা AB=h মিটার এবং প্রথম অবস্থান C থেকে টিলার পাদদেশ B পর্যন্ত অনুভূমিক দূরত্ব BC।
প্রথম অবস্থায়:
\tan45^\circ=\frac{AB}{BC}
\Rightarrow 1=\frac{h}{BC}
\Rightarrow BC=h …(i)
ঢাল বেয়ে অগ্রগমন:
30^\circ ঢালে 100 মিটার এগোনো হয়েছে।
উল্লম্ব সরণ
=100\sin30^\circ=100\times\frac{1}{2}=50 মিটার।
অনুভূমিক সরণ
=100\cos30^\circ=100\times\frac{\sqrt3}{2}=50\sqrt3 মিটার।
দ্বিতীয় অবস্থায়:
নতুন উচ্চতা
=h-50
নতুন অনুভূমিক দূরত্ব
=h-50\sqrt3
উন্নতি কোণ 60^\circ, সুতরাং
\tan60^\circ=\frac{h-50}{h-50\sqrt3}
\Rightarrow \sqrt3=\frac{h-50}{h-50\sqrt3}
\Rightarrow \sqrt3h-150=h-50
\Rightarrow h(\sqrt3-1)=100
\Rightarrow h=\frac{100}{\sqrt3-1}
হর মুক্ত করে পাই,
h=50(\sqrt3+1) মিটার।
দশমিক মানে:
\sqrt3\approx1.732
\Rightarrow h\approx50(1.732+1)=136.6 মিটার।
সঠিক উত্তর: টিলার উচ্চতা প্রায় 136.6 মিটার।
14. যে কোন দুটি প্রশ্নের উত্তর দাও:
(i) একটি নিরেট আয়ত ঘনকের দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 4:3:2 এবং সমগ্রতলের ক্ষেত্রফল 468 বর্গসেমি। আয়ত ঘনকের আয়তন নির্ণয় করো।
দৈর্ঘ্য =4x,
প্রস্থ =3x,
উচ্চতা =2x।
সমগ্রতলের ক্ষেত্রফল
=2(lb+bh+hl)
অতএব,
2\{(4x)(3x)+(3x)(2x)+(2x)(4x)\}=468
\Rightarrow 2(12x^2+6x^2+8x^2)=468
\Rightarrow 2(26x^2)=468
\Rightarrow 52x^2=468
\Rightarrow x^2=9
\Rightarrow x=3
সুতরাং,
দৈর্ঘ্য =12 সেমি,
প্রস্থ =9 সেমি,
উচ্চতা =6 সেমি।
আয়তন
=l\times b\times h
=12\times9\times6=648 ঘনসেমি।
সঠিক উত্তর: আয়ত ঘনকের আয়তন = 648 ঘনসেমি।
(ii) 20 সেমি উচ্চতা বিশিষ্ট একটি ফাঁপা চোঙের অন্তর্ব্যাসার্ধ ও বহির্ব্যাসার্ধ যথাক্রমে 4 সেমি ও 5 সেমি।
এই চোঙটিকে গলিয়ে চোঙের এক-তৃতীয়াংশ উচ্চতা বিশিষ্ট একটি নিরেট শঙ্কু তৈরি করা হল।
শঙ্কুটির ভূমিতলের ব্যাস নির্ণয় করো।
উচ্চতা, h_1 = 20 সেমি
বহির্ব্যাসার্ধ, R = 5 সেমি
অন্তর্ব্যাসার্ধ, r = 4 সেমি
ফাঁপা চোঙের আয়তন,
=\pi h_1 (R^2-r^2)
=\pi \times 20 \times (25-16)
=\pi \times 20 \times 9
=180\pi ঘনসেমি
2. নিরেট শঙ্কুর তথ্য:
উচ্চতা, h_2=\frac{1}{3}\times 20=\frac{20}{3} সেমি
ধরি, শঙ্কুর ভূমিতলের ব্যাসার্ধ = x সেমি।
শঙ্কুর আয়তন,
=\frac{1}{3}\pi x^2 h_2
=\frac{1}{3}\pi x^2\times\frac{20}{3}=\frac{20}{9}\pi x^2
3. শর্তানুসারে (আয়তন অপরিবর্তিত):
\frac{20}{9}\pi x^2=180\pi
\Rightarrow \frac{20}{9}x^2=180
\Rightarrow x^2=\frac{180\times 9}{20}
\Rightarrow x^2=81
\Rightarrow x=9 সেমি
4. শঙ্কুর ভূমিতলের ব্যাস:
=2x=2\times 9=18 সেমি
সঠিক উত্তর: শঙ্কুটির ভূমিতলের ব্যাস 18 সেমি
(iii) 9 সেমি অন্তর্ব্যাসার্ধ বিশিষ্ট একটি অর্ধগোলাকার পাত্র জলপূর্ণ আছে।
এই জল 3 সেমি ব্যাস ও 4 সেমি উচ্চতা বিশিষ্ট চোঙাকৃতি বোতলে ভর্তি করা হলে কতগুলি বোতল জলপূর্ণ হবে?
অন্তর্ব্যাসার্ধ, r = 9 সেমি
অর্ধগোলাকার পাত্রের আয়তন
=\frac{2}{3}\pi r^3
=\frac{2}{3}\times\pi\times 9^3
=\frac{2}{3}\times\pi\times 729
=486\pi ঘনসেমি
2. একটি চোঙাকৃতি বোতলের তথ্য:
ব্যাস = 3 সেমি
অতএব ব্যাসার্ধ, r_1=\frac{3}{2}=1.5 সেমি
উচ্চতা, h=4 সেমি
চোঙের আয়তন
=\pi r_1^2 h
=\pi\times(1.5)^2\times 4
=\pi\times 2.25\times 4
=9\pi ঘনসেমি
3. বোতলের সংখ্যা নির্ণয়:
ধরি, জলপূর্ণ বোতলের সংখ্যা = n
শর্তানুসারে,
n\times 9\pi = 486\pi
\Rightarrow n=\frac{486\pi}{9\pi}
\Rightarrow n=54
সঠিক উত্তর: 54টি বোতল জলপূর্ণ হবে।
15. যে কোন দুটি প্রশ্নের উত্তর দাও:
(i) নিচের তথ্যের গড় নির্ণয় করো।
শ্রেণী পরিসর
5–14
15–24
25–34
35–44
45–54
55–64
ছাত্রসংখ্যা
3
6
18
20
10
3
| শ্রেণী পরিসর | 5–14 | 15–24 | 25–34 | 35–44 | 45–54 | 55–64 |
| ছাত্রসংখ্যা | 3 | 6 | 18 | 20 | 10 | 3 |
| শ্রেণি (Class interval) | বারম্বারতা (f) |
|---|---|
| 5–14 | 3 |
| 15–24 | 6 |
| 25–34 | 18 |
| 35–44 | 20 |
| 45–54 | 10 |
| 55–64 | 3 |
1. শ্রেণি-মধ্যক (x) নির্ণয়:
| শ্রেণি | f | x | f × x |
|---|---|---|---|
| 5–14 | 3 | 9.5 | 28.5 |
| 15–24 | 6 | 19.5 | 117 |
| 25–34 | 18 | 29.5 | 531 |
| 35–44 | 20 | 39.5 | 790 |
| 45–54 | 10 | 49.5 | 495 |
| 55–64 | 3 | 59.5 | 178.5 |
2. মোট মান নির্ণয়:
\sum f = 3+6+18+20+10+3 = 60
3. গড় (Mean) নির্ণয়:
\text{Mean}=\frac{\sum fx}{\sum f}=\frac{2140}{60}
\Rightarrow \text{Mean}=35.67 (প্রায়)
সঠিক উত্তর: গড় ≈ 35.67
(ii) প্রদত্ত তথ্যের ক্রমযোজিত পরিসংখ্যা (বৃহত্তর সূচক) তালিকা তৈরি করে ছক কাগজে ওজাইভ অঙ্কন করো।
শ্রেণি
100–120
120–140
140–160
160–180
180–200
পরিসংখ্যা
8
14
10
12
4
| শ্রেণি | 100–120 | 120–140 | 140–160 | 160–180 | 180–200 |
| পরিসংখ্যা | 8 | 14 | 10 | 12 | 4 |
N = 8+14+10+12+4 = 48
2. বৃহত্তর সূচকের ক্রমযোজিত পরিসংখ্যা (More than cumulative frequency):
| শ্রেণি (Lower limit) | বৃহত্তর সূচক পরিসংখ্যা |
|---|---|
| >100 | 48 |
| >120 | 48 − 8 = 40 |
| >140 | 40 − 14 = 26 |
| >160 | 26 − 10 = 16 |
| >180 | 16 − 12 = 4 |
| >200 | 0 |
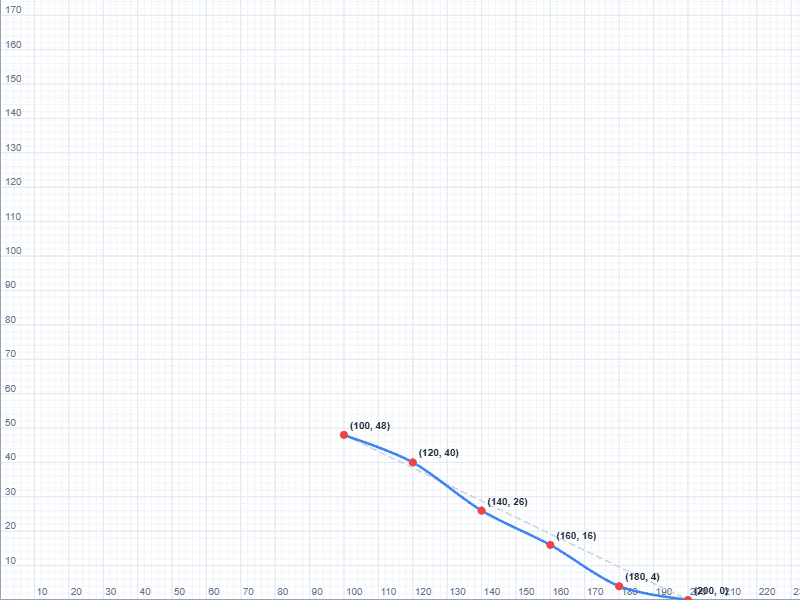
3. Ogive আঁকার জন্য প্রয়োজনীয় Coordination Points (x, y):
– (100, 48)
– (120, 40)
– (140, 26)
– (160, 16)
– (180, 4)
– (200, 0)
4. Ogive অঙ্কন পদ্ধতি:
– X-অক্ষে শ্রেণির নিম্নসীমা নাও।
– Y-অক্ষে বৃহত্তর সূচক পরিসংখ্যা নাও।
– উপরোক্ত বিন্দুগুলি ছক কাগজে চিহ্নিত করো।
– বিন্দুগুলিকে মসৃণ রেখা দিয়ে যুক্ত করলে বৃহত্তর সূচক Ogive পাওয়া যাবে।
(iii) নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির সংখ্যাগুরুমান নির্ণয় করো।
প্রাপ্ত নম্বর
10 এর কম
20 এর কম
30 এর কম
40 এর কম
50 এর কম
60 এর কম
শিক্ষার্থী সংখ্যা
8
15
29
42
60
70
| প্রাপ্ত নম্বর | 10 এর কম | 20 এর কম | 30 এর কম | 40 এর কম | 50 এর কম | 60 এর কম |
| শিক্ষার্থী সংখ্যা | 8 | 15 | 29 | 42 | 60 | 70 |
1. সাধারণ পরিসংখ্যা বিভাজন তালিকা
| শ্রেণি সীমানা | পরিসংখ্যা (f) |
|---|---|
| 0 – 10 | 8 |
| 10 – 20 | 15 − 8 = 7 |
| 20 – 30 | 29 − 15 = 14 |
| 30 – 40 | 42 − 29 = 13 |
| 40 – 50 | 60 − 42 = 18 |
| 50 – 60 | 70 − 60 = 10 |
2. সংখ্যাগুরুমান (Mode) নির্ণয়
এখানে সর্বোচ্চ পরিসংখ্যা হলো 18
অতএব, সংখ্যাগুরুমান সংবলিত শ্রেণি হলো 40 – 50
এক্ষেত্রে,
– সংখ্যাগুরুমান শ্রেণির নিম্নসীমা, l = 40
– সংখ্যাগুরুমান শ্রেণির পরিসংখ্যা, f_m = 18
– পূর্ববর্তী শ্রেণির পরিসংখ্যা, f_1 = 13
– পরবর্তী শ্রেণির পরিসংখ্যা, f_2 = 10
– শ্রেণি দৈর্ঘ্য, h = 10
সংখ্যাগুরুমানের সূত্র
Mode = l + \left( \frac{f_m - f_1}{2f_m - f_1 - f_2} \right) \times h
মান বসিয়ে পাই,
Mode = 40 + \left( \frac{18 - 13}{2 \times 18 - 13 - 10} \right) \times 10
= 40 + \left( \frac{5}{36 - 23} \right) \times 10 = 40 + \frac{50}{13} = 40 + 3.846 Mode [latex]= \approx 43.85সঠিক উত্তর:
তথ্যটির সংখ্যাগুরুমান ≈ 43.85
16. যে কোন একটি প্রশ্নের উত্তর দাও:
(i) একটি ত্রিভুজের পরিবৃত্ত অঙ্কন প্রণালী বর্ণনা করো।
1. প্রথমে প্রদত্ত ত্রিভুজটি অঙ্কন করি। ধরা যাক, ত্রিভুজটি \triangle ABC।
2. AB বাহুর লম্ব সমদ্বিখণ্ডক অঙ্কন করি।
অর্থাৎ, AB বাহুর মধ্যবিন্দু নির্ণয় করে সেখানে AB-এর উপর লম্ব একটি সরলরেখা অঙ্কন করি।
3. একইভাবে BC (অথবা AC) বাহুর লম্ব সমদ্বিখণ্ডক অঙ্কন করি।
4. এই দুটি লম্ব সমদ্বিখণ্ডক একটি বিন্দুতে ছেদ করবে। ধরা যাক, ছেদবিন্দুটি O।
এই O বিন্দুটি ত্রিভুজের পরিবৃত্তের কেন্দ্র।
5. এখন O বিন্দুকে কেন্দ্র করে এবং OA (বা OB, OC) ব্যাসার্ধ নিয়ে একটি বৃত্ত অঙ্কন করি।
তাহলে অঙ্কিত বৃত্তটি ত্রিভুজের তিনটি শীর্ষবিন্দু A, B, C-এর মধ্য দিয়ে অতিক্রম করবে।
এই বৃত্তটিই প্রদত্ত ত্রিভুজের পরিবৃত্ত।
(ii) একটি সমবাহু ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট একটি বর্গক্ষেত্রের অঙ্কন প্রণালী বর্ণনা করো।
একটি ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্র অঙ্কন করার জন্য প্রধানত দুটি ধাপ অনুসরণ করতে হয়।
ধাপ 1: ত্রিভুজের সমান ক্ষেত্রফল বিশিষ্ট আয়তক্ষেত্র অঙ্কন
1. প্রথমে প্রদত্ত বাহুর দৈর্ঘ্য অনুযায়ী সমবাহু ত্রিভুজ \triangle ABC অঙ্কন করি।
2. BC ভূমির সমান্তরাল করে শীর্ষবিন্দু A দিয়ে একটি সরলরেখা XY অঙ্কন করি।
3. BC বাহুকে লম্বভাবে সমদ্বিখণ্ডিত করি, যা BC-কে D বিন্দুতে ছেদ করে।
4. এই লম্ব সমদ্বিখণ্ডকটি সমান্তরাল রেখা XY-কে P বিন্দুতে ছেদ করে।
5. এখন C বিন্দুতে একটি লম্ব অঙ্কন করি যা XY রেখাকে Q বিন্দুতে ছেদ করে।
6. এভাবে প্রাপ্ত CDQP হলো একটি আয়তক্ষেত্র, যার ক্ষেত্রফল \triangle ABC-এর ক্ষেত্রফলের সমান।
ধাপ 2: আয়তক্ষেত্রের সমান ক্ষেত্রফল বিশিষ্ট বর্গক্ষেত্র অঙ্কন
(মধ্যসমানুপাতী পদ্ধতি)
1. আয়তক্ষেত্রের বড় বাহু CD-কে E বিন্দু পর্যন্ত বর্ধিত করি, যাতে
DE = DP হয় (আয়তক্ষেত্রের প্রস্থ)।
2. এখন CE রেখাকে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করি।
3. D বিন্দুতে CE-এর উপর একটি লম্ব অঙ্কন করি, যা অর্ধবৃত্তের পরিধিকে S বিন্দুতে ছেদ করে।
4. এই DS রেখাই হলো নির্ণেয় বর্গক্ষেত্রের বাহুর দৈর্ঘ্য।
5. এখন DS বাহুর সমান দৈর্ঘ্য নিয়ে একটি বর্গক্ষেত্র DSRT অঙ্কন করি।
উপসংহার:
অতএব, অঙ্কিত বর্গক্ষেত্র DSRT-এর ক্ষেত্রফল সমবাহু ত্রিভুজ \triangle ABC-এর ক্ষেত্রফলের সমান।
আমাদের লক্ষ্য সবসময় শিক্ষার্থীদের জন্য সঠিক ও নির্ভুল তথ্য প্রদান করা। তবুও অনিচ্ছাকৃতভাবে কোনো ভুল হয়ে গেলে, আমরা চাই সেটি যেন দ্রুত সংশোধন করা হয়।
যদি উপরের পোস্টটিতে কোনো ভুল বা অসঙ্গতি খুঁজে পান, অনুগ্রহ করে মন্তব্যে জানাবেন। আপনার সহযোগিতা আমাদের জন্য অমূল্য — কারণ আমরা চাই না কোনো শিক্ষার্থী ভুল শিখুক।
মনে রাখবেন: আপনার দেওয়া ছোট্ট একটি মন্তব্য অনেকের শেখার পথ সঠিক রাখতে সাহায্য করবে।