Class 6 Mathematics Chapter 01 Koshe Dekhi 1.5 Question Answer
ষষ্ঠ শ্রেণীর গণিতের প্রথম অধ্যায় “পূর্বপাঠের পুনরালোচনা” শিক্ষার্থীদের জন্য গুরুত্বপূর্ণ। এর “কষে দেখি ১.৫” অংশে জ্যামেতিক পরিমাপ গাণিতিক ক্রিয়ার অনুশীলন রয়েছে। এই অংশ শিক্ষার্থীদের আগের শ্রেণির ধারণাগুলো পুনরায় ঝালিয়ে নিতে সাহায্য করে। ধাপে ধাপে সমাধানের মাধ্যমে তারা সহজে বুঝতে পারে কিভাবে সমস্যার সমাধান করতে হয়। এই অনুশীলনগুলো যুক্তি ও বিশ্লেষণ ক্ষমতা বাড়ায় এবং ভবিষ্যতের গণিত অধ্যয়নের ভিত্তি শক্ত করে। এই ব্লগে আমরা “কষে দেখি ১.৫”-এর সব প্রশ্নের সহজ, স্পষ্ট ও ব্যাখ্যাসহ সমাধান তুলে ধরেছি যাতে শিক্ষার্থীরা সহজে শিখতে পারে।
1. কোণ গুলি ঠিক ঠিক ঘরে লেখার চেষ্টা করিঃ 12°, 22.5°,180°,179°,100°,39°,90°,69°,91°
| কোণসমূহ | কোণের প্রকার |
|---|---|
| 12°, 22.5°, 39°, 69° | সূক্ষ্মকোণ |
| 90° | সমকোণ |
| 180° | সরলকোণ |
| 91°, 100°, 179° | স্থূলকোণ |
2. সরলকোণ = 2 × তাই সরলকোণ, সমকোণের দ্বিগুণ।
সরলকোণ = 2 × 90° তাই সরলকোণ, সমকোণের দ্বিগুণ।
3. নিচের কোন কোন দৈর্ঘ্যের রেখাংশগুলির দ্বারা ত্রিভুজ তৈরি করা যায় দেখিঃ
অর্থাৎ, যদি তিনটি বাহু হয় a, b, এবং c, তাহলে শর্তগুলো হবে — a + b > c , b + c > a , c + a > b
(a) 2 সেমি, 3 সেমি, 4 সেমি
2 + 3 = 5 > 4
3 + 4 = 7 > 2
4 + 2 = 6 > 3
তিনটি ক্ষেত্রেই শর্ত পূরণ হচ্ছে।
অতএব, 2 cm, 3 cm, এবং 4 cm দৈর্ঘ্যের রেখাংশ দ্বারা ত্রিভুজ তৈরি করা যায়।
(b) 4 সেমি, 3 সেমি, 7 সেমি
4 + 3 = 7 = 7 (বেশি নয়)
3 + 7 = 10 > 4
7 + 4 = 11 > 3
একটি শর্ত পূরণ হচ্ছে না।
অতএব, 4 cm, 3 cm, এবং 7 cm দৈর্ঘ্যের রেখাংশ দ্বারা ত্রিভুজ তৈরি করা যায় না।
(c) 1 সেমি, 3 সেমি, 2 সেমি
4 + 3 = 7 = 7 (বেশি নয়)
3 + 7 = 10 > 4
7 + 4 = 11 > 3
একটি শর্ত পূরণ হচ্ছে না।
অতএব, 4 cm, 3 cm, এবং 7 cm দৈর্ঘ্যের রেখাংশ দ্বারা ত্রিভুজ তৈরি করা যায় না।
(d) সেমি, সেমি, সেমি
5 সেমি, 6 সেমি, 8 সেমি
5 + 6 = 11 > 8
6 + 8 = 14 > 5
8 + 5 = 13 > 6
তিনটি ক্ষেত্রেই শর্ত পূরণ হচ্ছে।
অতএব, 5 cm, 6 cm, এবং 8 cm দৈর্ঘ্যের রেখাংশ দ্বারা ত্রিভুজ তৈরি করা যায়।
4. সূক্ষ্মকোণী ও স্থূলকোণী ত্রিভুজ কাকে বলে লিখি এবং ছবি এঁকে চাঁদার সাহায্যে কোণগুলি মাপি।
সূক্ষ্মকোণী ত্রিভুজ (Acute-angled Triangle):
যে ত্রিভুজের তিনটি কোণই সূক্ষ্ম কোণ (অর্থাৎ 90°-এর কম) হয়, তাকে সূক্ষ্মকোণী ত্রিভুজ বলে।
উদাহরণ:
60°, 70°, এবং 50° কোণ বিশিষ্ট একটি ত্রিভুজ সূক্ষ্মকোণী ত্রিভুজ।
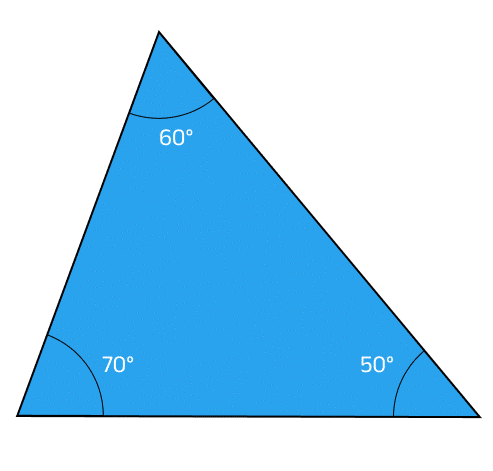
📏 চাঁদার সাহায্যে:
প্রতিটি কোণ মাপলে দেখা যায় — তিনটিই 90°-এর কম।
স্থূলকোণী ত্রিভুজ (Obtuse-angled Triangle):
যে ত্রিভুজের একটি কোণ স্থূল কোণ (অর্থাৎ 90°-এর বেশি কিন্তু 180°-এর কম) হয়, তাকে স্থূলকোণী ত্রিভুজ বলে।
উদাহরণ:
40°, 30°, এবং 110° কোণ বিশিষ্ট একটি ত্রিভুজ স্থূলকোণী ত্রিভুজ।
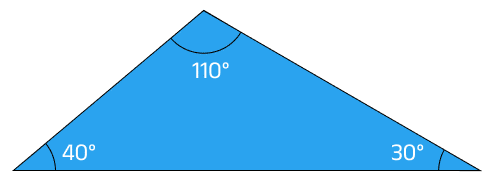
📏 চাঁদার সাহায্যে:
একটি কোণ 90°-এর বেশি পাওয়া যায়, তাই এটি স্থূলকোণী ত্রিভুজ।
5. নিচের বর্গাক্ষেত্রাকার চিত্রের পরিসিমা মাপিঃ

বৃত্তটি বর্গক্ষেত্রের ভেতরে অঙ্কিত, অর্থাৎ বৃত্তটি বর্গক্ষেত্রের চারটি বাহুর মাঝখানে স্পর্শ করছে।
তাহলে বৃত্তের ব্যাস = বর্গক্ষেত্রের বাহু = 4 সেমি
সূত্র:
বৃত্তের পরিসীমা = π × ব্যাস
অর্থাৎ,
পরিসীমা = 3.1416 × 4 = 12.5664 সেমি
বৃত্তের পরিসীমা ≈ 12.57 সেমি (দশমিকের দুই ঘর পর্যন্ত)
6. ওপরের বৃত্তাকার ক্ষেত্রের ব্যাস = সেমি।
ব্যাসার্ধ = সেমি। = সেমি।
বৃত্তাকার ক্ষেত্রের ব্যাস = 4 সেমি।
ব্যাসার্ধ = 4 \div 2 সেমি। = 2 সেমি।
আমাদের লক্ষ্য সবসময় শিক্ষার্থীদের জন্য সঠিক ও নির্ভুল তথ্য প্রদান করা। তবুও অনিচ্ছাকৃতভাবে কোনো ভুল হয়ে গেলে, আমরা চাই সেটি যেন দ্রুত সংশোধন করা হয়।
যদি উপরের পোস্টটিতে কোনো ভুল বা অসঙ্গতি খুঁজে পান, অনুগ্রহ করে মন্তব্যে জানাবেন। আপনার সহযোগিতা আমাদের জন্য অমূল্য — কারণ আমরা চাই না কোনো শিক্ষার্থী ভুল শিখুক।
মনে রাখবেন: আপনার দেওয়া ছোট্ট একটি মন্তব্য অনেকের শেখার পথ সঠিক রাখতে সাহায্য করবে।