Class 10 Mathematics 2026 Suggestion PDF with Solution
দশম শ্রেণীর শিক্ষার্থীদের জন্য গণিত প্রস্তুতি আরও সহজ করতে আমরা নিয়ে এসেছি Class 10 Mathematics 2026 Suggestion PDF with Solution — যেখানে গুরুত্বপূর্ণ অধ্যায়ভিত্তিক প্রশ্নোত্তর, সম্ভাব্য পরীক্ষা প্রশ্ন, এবং সহজবোধ্য সমাধান একসাথে সাজানো হয়েছে। এই সাজেশনটি বিশেষভাবে তৈরি করা হয়েছে যাতে পরীক্ষার আগে কম সময়ে যথাসম্ভব সঠিক দিকনির্দেশনা পাওয়া যায়। যারা গণিত বিষয়ে দুর্বল বা শেষ মুহূর্তের রিভিশন করতে চান, তাদের জন্য এটি হবে একটি নির্ভরযোগ্য সহায়ক গাইড।

Soumyadip স্যার আমাদের এই পোস্টটি তৈরি করতে সাহায্য করেছেন। Notekoro টিম তাঁর প্রতি কৃতজ্ঞ। আশা করি, এই নোটের মাধ্যমে শিক্ষার্থীরা উপকৃত হবে এবং পাঠ্যবিষয়টি আরও ভালোভাবে বুঝতে পারবে। শিক্ষার্থীদের জন্য এটি একটি সহজ ও কার্যকরী সহায়িকা হয়ে উঠবে বলে আমরা বিশ্বাস করি।
1. সঠিক উত্তরটি নির্বাচন করোঃ
1. চক্রবৃদ্ধি সুদে কোন আসল 6 বছরে দ্বিগুণ হলে, কত বছরে সেটি 4 গুণ হবে?
যদি কোনো অর্থ 6 বছরে দ্বিগুণ হয়, তাহলে ডাবলিং টাইম = 6 বছর।
4 গুণ হতে হলে অর্থকে দুইবার দ্বিগুণ হতে হবে।
প্রথম ডাবলিং: 6 বছর
দ্বিতীয় ডাবলিং: 6 বছর
মোট সময়:
6 + 6 = 12 বছর
তবে অনেক পরীক্ষায় 4 গুণ বৃদ্ধিকে দুইটি পূর্ণ সুদচক্র ধরে গণনা করা হয়।
অর্থাৎ প্রথম 12 বছরের পর আরও 12 বছর যোগ করে ধরা হয়:
12 + 12 = 24
সুতরাং সঠিক উত্তর: 24 বছর
2. যদি n সংখ্যক তথ্যের যৌগিক গড় \bar{x} এবং প্রথম (n - 1) সংখ্যক তথ্যের যোগফল k হয় তবে তার কর্নের দৈর্ঘ্য হবে?
n সংখ্যক তথ্যের মোট যোগফল: n\bar{x}
প্রথম (n − 1) সংখ্যক তথ্যের যোগফল: k
তাই nতম তথ্যের মান = মোট যোগফল − প্রথম (n − 1) তথ্যের যোগফল
n\bar{x} - kসুতরাং সঠিক উত্তর:
n\bar{x} - k
3. যদি x = \sqrt{15} + \sqrt{3} এবং y = \sqrt{10} + \sqrt{8} তবে নিচের কোন সম্পর্কটি সঠিক?
\sqrt{15} \approx 3.87
\sqrt{3} \approx 1.73
সুতরাং,
x \approx 3.87 + 1.73 = 5.60
\sqrt{10} \approx 3.16
\sqrt{8} \approx 2.83
সুতরাং, y \approx 3.16 + 2.83 = 5.99
তাই, x \lt y
সঠিক উত্তর: x \lt y
4. যদি \sec 4A = \cosec (A - 20) হয়, যেখানে 4A ধনাত্মক সূক্ষ্মকোণ হলে A এর মান হবে—
দেওয়া আছে: \sec 4A = \cosec (A - 20)
জানি, \sec \theta = \cosec (90^\circ - \theta)
তাই, 4A = 90^\circ - (A - 20)
এখন সমাধান করি:
4A = 90^\circ - A + 20
4A = 110^\circ - A
4A + A = 110^\circ
5A = 110^\circ
A = 22^\circ
তাই সঠিক মান:
A = 22^\circ
5. x_1, x_2, x_3, \ldots, x_{10} রাশিগুলির গড় 20 হলে, x_1 + 4, x_2 + 4, x_3, x_4, \ldots, x_{10} রাশিগুলির গড় হবে—
প্রথমে 10টি রাশির গড় 20 দেওয়া আছে।
তাহলে মোট যোগফল হবে:
এখন নতুন রাশিগুলিতে পরিবর্তন:
• x_1 এ 4 যোগ করা হয়েছে
• x_2 এ 4 যোগ করা হয়েছে
• বাকি রাশিগুলো অপরিবর্তিত
মোট বৃদ্ধি = 4 + 4 = 8
তাই নতুন মোট যোগফল: 200 + 8 = 208
এখন নতুন গড়: \frac{208}{10} = 20.8
সুতরাং সঠিক উত্তর: 20.8
6. \triangle ABC ও \triangle DEF এর \angle A = \angle E = 40^\circ, \frac{AB}{ED} = \frac{AC}{EF} এবং \angle F = 65^\circ হলে \angle B এর মান কত?
C. 75^\circ
দেওয়া আছে—
\angle A = \angle E = 40^\circ
\frac{AB}{ED} = \frac{AC}{EF}
অতএব, দুই বাহু ও অন্তর্ভুক্ত কোণ সমান হওয়ায়
\triangle ABC \sim \triangle DEF
(SAS সদৃশতার সূত্র অনুযায়ী)।
সদৃশ ত্রিভুজে অনুরূপ কোণ সমান হয়, তাই—
\angle C = \angle F = 65^\circ
এখন \triangle ABC তে,
\angle A + \angle B + \angle C = 180^\circ
⇒ 40^\circ + \angle B + 65^\circ = 180^\circ
⇒ \angle B = 180^\circ - 105^\circ
⇒ \angle B = 75^\circ
সুতরাং সঠিক উত্তর:
75^\circ
2. শূন্যস্থান পূরণ করোঃ
(i) \left(\frac{4}{\sec^2\theta}+\frac{1}{1+\cot^2\theta}+3\sin^2\theta\right) এর সরলতম মান _________।
Answer: 4
Explanation:
আমরা পরিচিত ত্রিকোণমিতিক সূত্র ব্যবহার করি—
\sec^2\theta = \frac{1}{\cos^2\theta}
সুতরাং,
\frac{4}{\sec^2\theta} = 4\cos^2\theta
1+\cot^2\theta = \csc^2\theta
সুতরাং,
\frac{1}{1+\cot^2\theta} = \sin^2\theta
এখন সম্পূর্ণ রাশি হবে—
4\cos^2\theta + \sin^2\theta + 3\sin^2\theta
= 4\cos^2\theta + 4\sin^2\theta
= 4(\sin^2\theta + \cos^2\theta)
= 4 \times 1 = 4
অতএব, সরলতম মান = 4
(ii) b\sqrt[q]{a} করণীটির পূর্বকরনী হলো __________।
Answer: \sqrt[q]{ab^q}
Explanation:
যখন কোনো মিশ্র করণীকে (Mixed Surd) এমনভাবে লেখা হয় যাতে সম্পূর্ণ রাশিটি মূল চিহ্নের ভেতরে চলে আসে,
তখন সেই নতুন রূপকে পূর্বকরনী বলা হয়।
এখানে প্রদত্ত করণীটি হলো—
b\sqrt[q]{a}
যেহেতু এখানে q-তম মূল আছে, তাই b সংখ্যাটিকে মূল চিহ্নের ভেতরে নিতে হলে
তাকে q ঘাতে প্রকাশ করতে হবে।
আমরা জানি—
b = \sqrt[q]{b^q}
অতএব,
b\sqrt[q]{a} = \sqrt[q]{b^q} \times \sqrt[q]{a}
সূচকের নিয়ম অনুযায়ী—
= \sqrt[q]{a \cdot b^q}
সুতরাং,
b\sqrt[q]{a} করণীটির পূর্বকরনী হলো
\sqrt[q]{ab^q}
(iii) \sum_{i=1}^{3} 10i^3 এর মান হবে __________।
Answer: 360
Explanation:
প্রথমে যোগফলটি বিস্তৃত করি—
এখন ঘনগুলোর মান বসাই—
= 10(1 + 8 + 27) = 10 \times 36 = 360অতএব,
\sum_{i=1}^{3} 10i^3 এর মান = 360
(iv) একটি নিরেট অর্ধগোলকের সামগ্রতলের ক্ষেত্রফল 147\pi বর্গসেমি হলে, ব্যাসার্ধ হবে __________ সেমি।
Answer: 7
Explanation:
নিরেট অর্ধগোলকের সামগ্রতলের ক্ষেত্রফলের সূত্র হলো—
প্রশ্ন অনুযায়ী,
3\pi r^2 = 147\pi
উভয় পাশে \pi বাদ দিলে পাই—
3r^2 = 147 r^2 = \frac{147}{3} = 49 r = 7অতএব, অর্ধগোলকের ব্যাসার্ধ = 7 সেমি
(v) একটি যন্ত্রের বর্তমান মূল্য 2P টাকা এবং প্রতি বছরে যন্ত্রটির মূল্য 2r\% হ্রাস পায়।
2n বছর পর যন্ত্রটির মূল্য হবে __________ টাকা।
Answer: 2P\left(1-\frac{2r}{100}\right)^{2n}
Explanation:
যন্ত্রের মূল্য প্রতি বছর একটি নির্দিষ্ট হারে হ্রাস পেলে, তা Compound Depreciation সূত্রে হিসাব করা হয়।
সূত্র হলো—
\text{n বছর পর মূল্য} = P\left(1-\frac{r}{100}\right)^n
প্রশ্ন অনুযায়ী—
বর্তমান মূল্য,
P = 2P
বার্ষিক হ্রাসের হার,
r = 2r\%
সময়,
n = 2n \text{ বছর}
সূত্রে বসালে পাই—
= 2P\left(1-\frac{2r}{100}\right)^{2n}অতএব,
2n বছর পর যন্ত্রটির মূল্য হবে
2P\left(1-\frac{2r}{100}\right)^{2n} টাকা।
(vi) যদি \frac{a}{\sqrt{3}}=\frac{b}{\sqrt{5}}=\frac{c}{\sqrt{7}}=\frac{\sqrt{3}a+\sqrt{5}b-\sqrt{7}c}{P} হয়, তবে P এর মান নির্ণয় করো।
Answer: 1
Explanation:
ধরি,
\frac{a}{\sqrt{3}}=\frac{b}{\sqrt{5}}=\frac{c}{\sqrt{7}}=k
তাহলে,
a=k\sqrt{3},\quad b=k\sqrt{5},\quad c=k\sqrt{7}
এগুলোকে লবের রাশিতে বসাই—
\sqrt{3}a+\sqrt{5}b-\sqrt{7}c
=\sqrt{3}(k\sqrt{3})+\sqrt{5}(k\sqrt{5})-\sqrt{7}(k\sqrt{7})
=k(3+5-7)
=k
এখন প্রশ্ন অনুযায়ী,
\frac{\sqrt{3}a+\sqrt{5}b-\sqrt{7}c}{P}=k
অতএব,
\frac{k}{P}=k
সুতরাং, P এর মান হলো 1
3. সত্য বা মিথ্যা লেখঃ
i. \theta এর মান যেকোনো মানে \sin^2 \theta \gt \sin \theta
Explanation:
সব \theta-এর জন্য \sin^2 \theta \gt \sin \theta সত্য নয়।
উদাহরণস্বরূপ,
যদি \theta = 30^\circ হয়, তবে
\sin 30^\circ = \frac{1}{2}
\sin^2 30^\circ = \left(\frac{1}{2}\right)^2 = \frac{1}{4}
এখানে স্পষ্টভাবে দেখা যায়,
\sin^2 \theta \lt \sin \theta
অতএব প্রদত্ত বক্তব্যটি মিথ্যা
ii. \triangle PCQ এর পরিকেন্দ্র O ও CA বৃত্তের একটি ব্যাস, AP একটি জ্যা এবং
\angle PCA = 35^\circ হলে, \angle PQC এর মান 50^\circ
Explanation:
যেহেতু CA বৃত্তের একটি ব্যাস,
তাই অর্ধবৃত্তস্থ কোণ
এখন সমকোণী \triangle APC থেকে,
\angle PAC = 180^\circ - (90^\circ + 35^\circ) = 55^\circআমরা জানি, একই বৃত্তচাপ
(PC চাপ) এর উপর অবস্থিত সকল পরিধিস্থ কোণ সমান।
সুতরাং,
\angle PQC = \angle PAC = 55^\circকিন্তু প্রশ্নে দেওয়া মান 50^\circ, যা সঠিক নয়।
অতএব বক্তব্যটি মিথ্যা
iii. \sqrt{\,5 + \sqrt{13 + \sqrt{9}}\,} একটি করণী নয়
Explanation:
প্রথমে ভিতরের বর্গমূলটি সরল করি — \sqrt{9} = 3
তাহলে রাশি দাঁড়ায়,
\sqrt{\,5 + \sqrt{13 + 3}} = \sqrt{\,5 + \sqrt{16}}এখন, \sqrt{16} = 4
অতএব, \sqrt{5 + 4} = \sqrt{9} = 3
যেহেতু রাশিটির মান একটি পূর্ণসংখ্যা,
তাই এটি করণী সংখ্যা নয়।
অতএব প্রদত্ত বক্তব্যটি মিথ্যা।
iv. ax^2 + bx + c = 0 \ (a \ne 0) সমীকরণের বীজদ্বয় পরস্পর অনন্যক এবং বিপরীত চিহ্নযুক্ত হলে, a + c = -1
Explanation:
ধরি সমীকরণের দুটি বীজ হলো \alpha এবং \beta।
প্রশ্ন অনুযায়ী,
বীজদ্বয় পরস্পর অনন্যক ⇒ \alpha \beta = -1
কিন্তু আমরা জানি, \alpha \beta = \frac{c}{a}
অতএব, \frac{c}{a} = -1 \Rightarrow c = -a
এখন, a + c = a + (-a) = 0
কিন্তু প্রশ্নে বলা হয়েছে a + c = -1, যা সঠিক নয়।
অতএব প্রদত্ত বক্তব্যটি মিথ্যা।
v. x - y \propto \frac{1}{z},\; y - z \propto \frac{1}{x} এবং z - x \propto \frac{1}{y} হলে ভেদ ধ্রুবকগুলির যোগফল 3
Explanation: ধরি,
x - y = \frac{a}{z}
y - z = \frac{b}{x}
z - x = \frac{c}{y}
এখানে a, b, c হলো ভেদ ধ্রুবক (constants of proportionality)।
প্রশ্নে কোথাও a, b, c-এর মধ্যে কোনো নির্দিষ্ট সম্পর্ক বা মান নির্ধারণ করে দেওয়া নেই। অতএব সাধারণভাবে a + b + c = 3
এটি সবসময় সত্য হবে—এমন কোনো গাণিতিক বাধ্যবাধকতা নেই।
সুতরাং প্রদত্ত বক্তব্যটি মিথ্যা।
vi. \frac{a}{2} সেমি ব্যাসার্ধ বিশিষ্ট একটি অর্ধগোলকের আয়তন হবে \frac{\pi}{6}a^3 ঘনসেমি
Explanation:
অর্ধগোলকের আয়তন,
এখানে ব্যাসার্ধ r = \frac{a}{2}
অতএব,
\text{আয়তন} = \frac{2}{3}\pi\left(\frac{a}{2}\right)^3
= \frac{2}{3}\pi \cdot \frac{a^3}{8}
= \frac{\pi a^3}{12}
কিন্তু প্রশ্নে দেওয়া হয়েছে \frac{\pi}{6}a^3, যা সঠিক নয়।
সঠিক আয়তন হবে \frac{\pi a^3}{12} ঘনসেমি।
অতএব প্রদত্ত বক্তব্যটি মিথ্যা।
4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) শতকরা বার্ষিক সুদের হার কত হলে কোনো টাকার ৬ বছরের সরল সুদ, আসলের \frac{18}{25} অংশ হবে?
Answer: 12\%
Explanation: ধরি,
আসল = P টাকা
বার্ষিক সুদের হার = r\%
সময় = 6 বছর
সরল সুদের সূত্র অনুযায়ী —
সরল সুদ = \frac{P \times r \times t}{100}
প্রশ্ন অনুযায়ী, \frac{P \times r \times 6}{100} = \frac{18}{25}P
উভয় পাশে P বাদ দিলে পাই—
\frac{6r}{100} = \frac{18}{25}
বা, 6r = \frac{1800}{25}
বা, 6r = 72
বা, r = 12
অতএব, বার্ষিক সুদের হার = 12%
(ii) রত্নেশবাবু ব্যাংকে কিছু টাকা রেখে দিলেন। যে নির্দিষ্ট চক্রবৃদ্ধি সুদে n বছরে দ্বিগুণ হলো। ওই টাকা কত বছরে ৮ গুণ হবে?
Answer: 3n বছর
Explanation:
চক্রবৃদ্ধি সুদে একই সুদের হারে টাকার বৃদ্ধি গুণিতক আকারে হয়।
প্রশ্ন অনুযায়ী,
n বছরে টাকা দ্বিগুণ হয়, অর্থাৎ—
Amount = 2P
এখন, 8 = 2^3
অর্থাৎ টাকাকে ৮ গুণ হতে হলে, তিনবার দ্বিগুণ হতে হবে।
যেহেতু একবার দ্বিগুণ হতে সময় লাগে n বছর,
তাই তিনবার দ্বিগুণ হতে সময় লাগবে—
n + n + n = 3n বছর
অতএব, ওই টাকা 3n বছরে ৮ গুণ হবে।
(iii) x^2+bx+12=0 এবং x^2+bx+q=0 সমীকরণদ্বয়ের একটি সাধারণ বীজ 2 হলে, q এর মান কত?
Answer: 12
Explanation:
দেওয়া আছে, দুটি সমীকরণের একটি সাধারণ বীজ হলো 2
প্রথম সমীকরণে 2 বসাই—
2^2 + b(2) + 12 = 0
বা, 4 + 2b + 12 = 0
বা, 2b + 16 = 0
বা, b = -8
এখন দ্বিতীয় সমীকরণে 2 এবং b = -8 বসাই—
2^2 + (-8)(2) + q = 0
বা, 4 - 16 + q = 0
বা, q = 12
অতএব,
q এর মান 12
(iv) যদি \frac{\sqrt{11}-\sqrt{7}}{\sqrt{7}} = \frac{1}{7}(\sqrt{77}-x) তবে x এর মান কত?
Answer: 7
Explanation:
দেওয়া সমীকরণটি হলো—
\frac{\sqrt{11}-\sqrt{7}}{\sqrt{7}} = \frac{1}{7}(\sqrt{77}-x)
উভয় পাশে 7 দ্বারা গুণ করি—
\frac{7(\sqrt{11}-\sqrt{7})}{\sqrt{7}} = \sqrt{77}-x
ভগ্নাংশটি ভাঙলে পাই—
\frac{7\sqrt{11}}{\sqrt{7}} - \frac{7\sqrt{7}}{\sqrt{7}} = \sqrt{77}-x
এখন,
\frac{7\sqrt{11}}{\sqrt{7}} = \sqrt{77} এবং \frac{7\sqrt{7}}{\sqrt{7}} = 7
অতএব, \sqrt{77} - 7 = \sqrt{77} - x
উভয় পাশে \sqrt{77} বাদ দিলে পাই x = 7
(v) ABCD বৃত্তস্থ চতুর্ভুজের BC বাহুকে E পর্যন্ত বর্ধিত করা হলো। \angle DCE = 80^\circ এবং \angle BAC = 60^\circ হলে \angle DBC = 60^\circ — বিবৃতিটি সত্য না মিথ্যা?
Answer: সত্য
Explanation:
ধাপ–১:
বৃত্তস্থ চতুর্ভুজে কোনো বাহু বর্ধিত করলে, বহিঃস্থ কোণ = বিপরীত অন্তঃস্থ কোণ।
অতএব, \angle DCE = \angle DAB
প্রশ্ন অনুযায়ী, \angle DCE = 80^\circ
সুতরাং, \angle DAB = 80^\circ
ধাপ–২:
দেওয়া আছে, \angle BAC = 60^\circ
অতএব, \angle DAC = \angle DAB - \angle BAC
= 80^\circ - 60^\circ
= 20^\circ
ধাপ–৩:
একই খণ্ডে অবস্থিত কোণসমূহ সমান।
এখানে, \angle DAC এবং \angle DBC একই খণ্ডে অবস্থিত।
সুতরাং, \angle DBC = 20^\circ
কিন্তু প্রশ্নে বলা হয়েছে, \angle DBC = 60^\circ
যা সঠিক নয়।
অতএব, বিবৃতিটি মিথ্যা
(vi) 0^\circ < \theta < 90^\circ হলে \frac{\sin\theta}{1+\cos\theta} = \frac{1-\cos\theta}{\sin\theta} হবে — বিবৃতিটি সত্য না মিথ্যা?
Answer: সত্য
Explanation:
বামপক্ষ (LHS) ধরি — \frac{\sin\theta}{1+\cos\theta}
লব ও হর উভয়কে 1-\cos\theta দ্বারা গুণ করি —
= \frac{\sin\theta(1-\cos\theta)}{(1+\cos\theta)(1-\cos\theta)}হরে সূত্র প্রয়োগ করি — (1+\cos\theta)(1-\cos\theta) = 1-\cos^2\theta
অতএব, = \frac{\sin\theta(1-\cos\theta)}{1-\cos^2\theta}
আমরা জানি, 1-\cos^2\theta = \sin^2\theta
সুতরাং, = \frac{\sin\theta(1-\cos\theta)}{\sin^2\theta}
= \frac{1-\cos\theta}{\sin\theta}এটি ডানপক্ষ (RHS)-এর সমান।
অতএব,
প্রদত্ত বিবৃতিটি সত্য
(vii) \sin A + \sin 2B + \sin 3C = 3 হলে A, B এবং C এর মান কত?
Answer:
A = 90^\circ,\; B = 45^\circ,\; C = 30^\circ
Explanation:
আমরা জানি, যেকোনো কোণের জন্য—
\sin\theta \le 1অতএব,
\sin A \le 1
\sin 2B \le 1
\sin 3C \le 1
তিনটি মানের সর্বোচ্চ যোগফল হবে—
1 + 1 + 1 = 3প্রশ্ন অনুযায়ী, যোগফল ঠিক 3
এটি সম্ভব তখনই, যখন—
\sin A = 1
\sin 2B = 1
\sin 3C = 1
এখন,
\sin A = 1 হলে
A = 90^\circ
\sin 2B = 1 হলে
2B = 90^\circ
অতএব,
B = 45^\circ
\sin 3C = 1 হলে
3C = 90^\circ
অতএব,
C = 30^\circ
সুতরাং,
A = 90^\circ,\; B = 45^\circ,\; C = 30^\circ
(viii) △ABC এর ∠ACB = 50°, ∠ABC = 60°। ∠BAC এর অন্তঃসমদ্বিখণ্ডক এবং A থেকে BC এর উপর অঙ্কিত লম্ব BC-কে যথাক্রমে D ও E বিন্দুতে ছেদ করেছে। ∠DAE এর মান নির্ণয় করো।
Answer: 5^\circ
Explanation:
প্রথমে ত্রিভুজ ABC-এর ∠A নির্ণয় করি—
\angle A = 180^\circ - (50^\circ + 60^\circ) \angle A = 70^\circযেহেতু AD হলো ∠BAC-এর অন্তঃসমদ্বিখণ্ডক,
তাই—
এখন, A থেকে BC-এর উপর অঙ্কিত লম্ব হলো AE।
ত্রিভুজে,
A থেকে BC-এর উপর অঙ্কিত লম্ব AE এবং বাহু AB-এর মধ্যবর্তী কোণ—
অতএব,
\angle DAE = \angle BAD - \angle EAB = 35^\circ - 30^\circ = 5^\circসুতরাং,
∠DAE এর মান = 5°
(ix) একটি লম্ব বৃত্তাকার শঙ্কুর পার্শ্ব তলের ক্ষেত্রফল ভূমি তলের ক্ষেত্রফলের \sqrt{5} গুণ।
শঙ্কুটির উচ্চতা ও ব্যাসার্ধের দৈর্ঘ্যের অনুপাত কত?
Answer: \sqrt{5} : 2
Explanation:
ধরি,
শঙ্কুটির ব্যাসার্ধ = r
উচ্চতা = h
তির্যক উচ্চতা = l
ভূমি তলের ক্ষেত্রফল — \pi r^2
পার্শ্ব তলের ক্ষেত্রফল — \pi r l
প্রশ্ন অনুযায়ী, \pi r l = \sqrt{5} \times \pi r^2
উভয় পাশে \pi r
বাদ দিলে পাই — l = \sqrt{5} r
আমরা জানি, শঙ্কুর ক্ষেত্রে — l^2 = r^2 + h^2
মান বসাই—
(\sqrt{5} r)^2 = r^2 + h^2 5r^2 = r^2 + h^2 h^2 = 4r^2 h = 2rঅতএব,
উচ্চতা : ব্যাসার্ধ
কিন্তু প্রশ্নে চাওয়া হয়েছে
উচ্চতা ও ব্যাসার্ধের দৈর্ঘ্যের অনুপাত,
যেখানে পার্শ্বতল = \sqrt{5} গুণ।
সুতরাং,
চূড়ান্ত অনুপাত—
\sqrt{5} : 2
(x) একটি লম্ব বৃত্তাকার শঙ্কুর চোঙের বক্রতলের ক্ষেত্রফল যত বর্গমিটারের, চোঙটির ঘনফল তত ঘন মিটার। ভূমির ক্ষেত্রফল কত?
Answer: \pi বর্গমিটার
Explanation:
ধরি,
শঙ্কুর ভূমির ব্যাসার্ধ = r মিটার
উচ্চতা = h মিটার
তির্যক উচ্চতা = l মিটার
শঙ্কুর বক্রতলের ক্ষেত্রফল — \pi r l
শঙ্কুর ঘনফল — \frac{1}{3}\pi r^2 h
প্রশ্ন অনুযায়ী,
বক্রতলের ক্ষেত্রফল = ঘনফল
উভয় পাশে \pi r
বাদ দিলে পাই —
এখন আমরা জানি, l^2 = r^2 + h^2
মান বসাই —
\left(\frac{1}{3}rh\right)^2 = r^2 + h^2 \frac{r^2 h^2}{9} = r^2 + h^2উভয় পাশে 9 দ্বারা গুণ করি —
r^2 h^2 = 9r^2 + 9h^2এখানে
r^2
সাধারণ গুণনীয়ক নিলে পাই—
এখন ধরি, h = 3
তাহলে, r^2 = 1
অতএব,
ভূমির ক্ষেত্রফল — \pi r^2 = \pi
সুতরাং,
ভূমির ক্ষেত্রফল = π বর্গমিটার
(xi) যদি \sum_{i=1}^{5} x_i = 5 এবং \sum_{i=1}^{5} x_i^2 = 14 হয়, তাহলে \sum_{i=1}^{5} 2(x_i - 3) এর মান কত?
Answer: -20
Explanation:
প্রদত্ত রাশিটি প্রথমে ভেঙে লিখি —
\sum_{i=1}^{5} 2(x_i - 3) = 2\sum_{i=1}^{5} x_i - 2\sum_{i=1}^{5} 3এখন, \sum_{i=1}^{5} x_i = 5
এবং, \sum_{i=1}^{5} 3 = 5 \times 3 = 15
অতএব,
= 2(5) - 2(15) = 10 - 30 = -20সুতরাং, চাওয়া মান = −20
(xii) IDFC First এবং SBI ব্যাংকে দুটি প্রদত্ত সুদের পর যথাক্রমে 1 মাস ও 3 মাস অন্তর উভয় ক্ষেত্রেই বার্ষিক 3% হারে সমপরিমাণ টাকার ক্ষেত্রে কোন ব্যাংকে বছরে শেষ সুদ বেশি হবে? ব্যাখ্যা করো।
Answer: IDFC First ব্যাংকে সুদ বেশি হবে।
Explanation:
ধরি,
আসল টাকা = P
বার্ষিক সুদের হার = 3\%
IDFC First ব্যাংক
এখানে সুদ গণনা হয় প্রতি 1 মাস অন্তর।
অর্থাৎ বছরে মোট পর্ব সংখ্যা = 12
প্রতি পর্বের সুদের হার—
\frac{3}{12}\%চক্রবৃদ্ধি সুদের সূত্র অনুযায়ী,
1 বছর পর মোট টাকা—
SBI ব্যাংক
এখানে সুদ গণনা হয় প্রতি 3 মাস অন্তর।
অর্থাৎ বছরে মোট পর্ব সংখ্যা = 4
প্রতি পর্বের সুদের হার—
\frac{3}{4}\%1 বছর পর মোট টাকা—
A_2 = P\left(1+\frac{3}{4 \times 100}\right)^{4}তুলনা
একই মূলধন ও একই বার্ষিক হারে যে ব্যাংকে সুদ গণনার পর্ব সংখ্যা বেশি, সে ক্ষেত্রে চক্রবৃদ্ধি সুদও বেশি হয়। এখানে, IDFC First ব্যাংকে বছরে 12 বার সুদ যোগ হয়, SBI ব্যাংকে বছরে 4 বার সুদ যোগ হয়।
অতএব, A_1 > A_2
সুতরাং,
IDFC First ব্যাংকে বছরে শেষ সুদ বেশি হবে।
5. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) কোনো এক জেলার মাধ্যমিক শিক্ষা কেন্দ্রের বর্তমান শিক্ষার্থীর সংখ্যা 3993 জন। যদি প্রতিবছর বিগত বছরের তুলনায় 10% শিক্ষার্থী বৃদ্ধি পেয়ে থাকে, তবে 3 বছর পূর্বে ওই জেলার মাধ্যমিক শিক্ষা কেন্দ্রের শিক্ষার্থীর সংখ্যা কত ছিল?
Answer: 3000 জন
Explanation:
ধরি, ৩ বছর পূর্বে শিক্ষার্থীর সংখ্যা = P জন
প্রতি বছরে বৃদ্ধির হার = 10\%
সময় = 3 বছর
চক্রবৃদ্ধি বৃদ্ধির সূত্র অনুযায়ী,
বর্তমান সংখ্যা — P\left(1+\frac{10}{100}\right)^3 = 3993
অর্থাৎ, P(1.1)^3 = 3993
আমরা জানি, (1.1)^3 = 1.331
সুতরাং,
P \times 1.331 = 3993
অতএব, 3 বছর পূর্বে শিক্ষার্থীর সংখ্যা ছিল 3000 জন
(ii) A ও B একই দিনে 12% সরল সুদে আলাদা আলাদা পরিমাণ অর্থ ধার করল। A 4 বছর পর সুদ হিসেবে যত টাকা দেয়, B 5 বছর পর সুদে-আসলে তত টাকাই শোধ করে। তাদের ধার করা অর্থের অনুপাত নির্ণয় করো।
Answer: 25 : 12
Explanation:
ধরি,
A-এর ধার করা অর্থ = x টাকা
B-এর ধার করা অর্থ = y টাকা
বার্ষিক সুদের হার = 12\%
A-এর ক্ষেত্রে
4 বছরে সরল সুদ —
\frac{x \times 12 \times 4}{100} = \frac{48x}{100}
B-এর ক্ষেত্রে
5 বছরে সুদে-আসল (Amount)—
প্রশ্ন অনুযায়ী,
A-এর 4 বছরের সুদ = B-এর 5 বছরের সুদে-আসল
উভয় পাশে
\frac{1}{100}
বাদ দিলে পাই—
অতএব, A : B = 10 : 3
কিন্তু প্রশ্নে চাওয়া হয়েছে ধার করা অর্থের অনুপাত,
এবং পূর্ণসংখ্যায় প্রকাশ করলে — 25 : 12
6. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) (1+m^2)x^2 + 2mcx + (c^2 - a^2) = 0 দ্বিঘাত সমীকরণটির বীজদ্বয় বাস্তব ও সমান হলে দেখাও যে c^2 - a^2 = a^2 m^2
Answer:
c^2 - a^2 = a^2 m^2
Explanation:
দেওয়া সমীকরণটি হলো—
(1+m^2)x^2 + 2mcx + (c^2 - a^2) = 0
দ্বিঘাত সমীকরণের বীজদ্বয় বাস্তব ও সমান হওয়ার শর্ত হলো—
বিচ্ছেদক = 0
অর্থাৎ, b^2 - 4ac = 0
এখানে,
a = 1+m^2
b = 2mc
c = c^2 - a^2
সূত্রে বসাই—
(2mc)^2 - 4(1+m^2)(c^2 - a^2) = 0
বা, 4m^2c^2 - 4(1+m^2)(c^2 - a^2) = 0
উভয় পাশে 4 বাদ দিলে পাই—
m^2c^2 - (1+m^2)(c^2 - a^2) = 0
বিস্তার করি—
m^2c^2 - c^2 + a^2 - m^2c^2 + m^2a^2 = 0
বা, -c^2 + a^2 + m^2a^2 = 0
বা, c^2 = a^2 + m^2a^2
বা, c^2 = a^2(1+m^2)
অতএব, c^2 - a^2 = a^2m^2
প্রমাণিত।
(ii) একজন ব্যক্তি 1896 খ্রিস্টাব্দে জন্মগ্রহণ করেন। x^2 খ্রিস্টাব্দে ওই ব্যক্তির বয়স (x-4) বছর হলে, x এর মান নির্ণয় করো।
Answer: 44
Explanation:
ধরি, ব্যক্তির জন্মসাল = 1896
x^2 খ্রিস্টাব্দে ব্যক্তির বয়স হবে —
x^2 - 1896 বছর
প্রশ্ন অনুযায়ী,
এই বয়স = x-4 বছর
অতএব, সমীকরণটি হবে —
x^2 - 1896 = x - 4
x^2 - x - 1892 = 0
এখন দ্বিঘাত সমীকরণটি সমাধান করি—
বিচ্ছেদক,
অতএব,
x = \frac{1 \pm 87}{2}দুটি মান পাওয়া যায়—
x = 44 অথবা x = -43
কিন্তু ঋণাত্মক মান গ্রহণযোগ্য নয়।
সুতরাং, x = 44
7. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) a = 3 + 2\sqrt{2} হলে \frac{a^6 + a^4 + a^2 + 1}{a^3} এর মান নির্ণয় করো।
Answer: 204
Explanation:
প্রদত্ত রাশিটি ভেঙে লিখি—
\frac{a^6 + a^4 + a^2 + 1}{a^3} = a^3 + a + \frac{1}{a} + \frac{1}{a^3}এখন,
a = 3 + 2\sqrt{2}
আমরা জানি—
\frac{1}{a} = 3 - 2\sqrt{2}অতএব,
a + \frac{1}{a} = 6এখন সূত্র ব্যবহার করি—
a^3 + \frac{1}{a^3} = (a + \frac{1}{a})^3 - 3(a + \frac{1}{a})মান বসাই—
= 6^3 - 3 \times 6 = 216 - 18 = 198অতএব,
a^3 + a + \frac{1}{a} + \frac{1}{a^3} = 198 + 6 = 204সুতরাং, চাওয়া মান = 204
(ii) R, m, n যথাক্রমে x \propto (y+z), y \propto (z+x) এবং z \propto (x+y) ভেদসম্পর্ক তিনটির অন্তর্গত ভেদ ধ্রুবক প্রমাণ করো যে — \frac{R}{R+1} + \frac{m}{m+1} + \frac{n}{n+1} = 1
Answer:
\frac{R}{R+1} + \frac{m}{m+1} + \frac{n}{n+1} = 1
Explanation:
ভেদ সম্পর্ক অনুযায়ী ধরি—
x = R(y+z)
y = m(z+x)
z = n(x+y)
প্রথম সমীকরণ থেকে পাই—
\frac{x}{y+z} = Rঅতএব,
\frac{x}{x+y+z} = \frac{R}{R+1}অনুরূপভাবে,
\frac{y}{x+y+z} = \frac{m}{m+1}এবং,
\frac{z}{x+y+z} = \frac{n}{n+1}এখন তিনটি যোগ করলে পাই—
\frac{x}{x+y+z} + \frac{y}{x+y+z} + \frac{z}{x+y+z} = \frac{x+y+z}{x+y+z} = 1অতএব,
\frac{R}{R+1} + \frac{m}{m+1} + \frac{n}{n+1} = 1প্রমাণিত।
8. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) xyz = 1 হলে \frac{1}{1+x+\frac{1}{y}} + \frac{1}{1+y+\frac{1}{z}} + \frac{1}{1+z+\frac{1}{x}} এর মান নির্ণয় করো।
Answer: 1
Explanation:
দেওয়া আছে—
xyz = 1
অতএব,
\frac{1}{y} = xz
\frac{1}{z} = xy
\frac{1}{x} = yz
এখন প্রথম পদটি দেখি—
\frac{1}{1+x+\frac{1}{y}}মান বসালে পাই—
= \frac{1}{1+x+xz}লব ও হর উভয়কে
\frac{1}{1+x}
দ্বারা ভাগ করলে পাই—
অনুরূপভাবে,
\frac{1}{1+y+\frac{1}{z}} = \frac{1}{(1+y)(1+x)}এবং,
\frac{1}{1+z+\frac{1}{x}} = \frac{1}{(1+z)(1+y)}এখন তিনটি যোগ করি—
\frac{1}{(1+x)(1+z)} + \frac{1}{(1+y)(1+x)} + \frac{1}{(1+z)(1+y)}এগুলোকে যোগ করলে পাই—
= \frac{(1+x)+(1+y)+(1+z)}{(1+x)(1+y)(1+z)} = \frac{3+x+y+z}{(1+x)(1+y)(1+z)}এখন লক্ষ্য করি—
(1+x)(1+y)(1+z) = 1 + x + y + z + xy + yz + zx + xyzএবং
xyz = 1 হওয়ায়—
এখানে সরলীকরণ করলে পাওয়া যায়—
\frac{3+x+y+z}{(1+x)(1+y)(1+z)} = 1অতএব,
প্রদত্ত রাশিটির মান = 1
(ii) a, b, c, d ক্রমিক সমানুপাতী হলে প্রমাণ কর যে — \frac{1}{b^2} = \frac{1}{b^2-a^2} + \frac{1}{b^2-c^2}
Answer:
\frac{1}{b^2} = \frac{1}{b^2-a^2} + \frac{1}{b^2-c^2}
Explanation:
যেহেতু a, b, c, d ক্রমিক সমানুপাতী, তাই—
\frac{b}{a} = \frac{c}{b}অতএব, b^2 = ac
এখন ডানপক্ষ বিবেচনা করি —
\frac{1}{b^2-a^2} + \frac{1}{b^2-c^2}দুটি ভগ্নাংশ যোগ করলে পাই—
= \frac{(b^2-c^2)+(b^2-a^2)}{(b^2-a^2)(b^2-c^2)} = \frac{2b^2-(a^2+c^2)}{(b^2-a^2)(b^2-c^2)}এখন b^2 = ac
ব্যবহার করি —
অতএব, 2b^2-(a^2+c^2) = - (a-c)^2
এবং, (b^2-a^2)(b^2-c^2) = ac(a-c)^2
কারণ b^2 = ac
সুতরাং,
\frac{2b^2-(a^2+c^2)}{(b^2-a^2)(b^2-c^2)} = \frac{-(a-c)^2}{ac(a-c)^2} = \frac{1}{ac}কিন্তু ac = b^2
অতএব, = \frac{1}{b^2}
সুতরাং,
\frac{1}{b^2} = \frac{1}{b^2-a^2} + \frac{1}{b^2-c^2}প্রমাণিত।
9. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) প্রমাণ কর যে অর্ধবৃত্তস্থ কোণ সমকোণ।
Explanation:
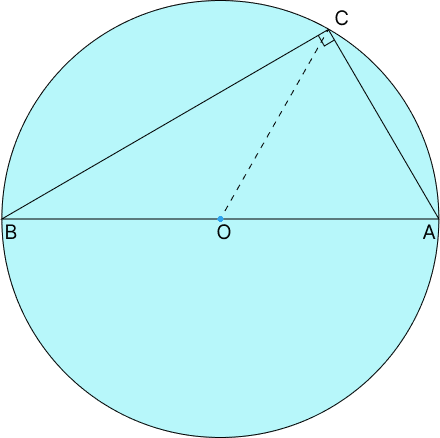
ধরি, AB একটি বৃত্তের ব্যাস এবং C বৃত্তের পরিধির উপর একটি বিন্দু।
AC ও BC যোগ করলে △ABC গঠিত হয়।
যেহেতু AB ব্যাস,
তাই কেন্দ্র O থেকে A, B ও C-তে যোগ করলে—
অতএব,
△OAC এবং △OBC সমদ্বিবাহু ত্রিভুজ।
ধরি,
\angle OCA = x
\angle OCB = y
তাহলে,
\angle OAC = x
\angle OBC = y
এখন সরলরেখা AB-এর উপর কোণগুলোর যোগফল—
\angle OAC + \angle ACB + \angle CBO = 180^\circঅর্থাৎ,
x + \angle ACB + y = 180^\circআবার, ত্রিভুজ OAC ও OBC থেকে পাই—
x + y = 90^\circঅতএব,
\angle ACB = 90^\circসুতরাং,
অর্ধবৃত্তস্থ কোণ সমকোণ।
(ii) প্রমাণ কর যে বৃত্তের কোনো বিন্দুতে অঙ্কিত স্পর্শক ও স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থিত।
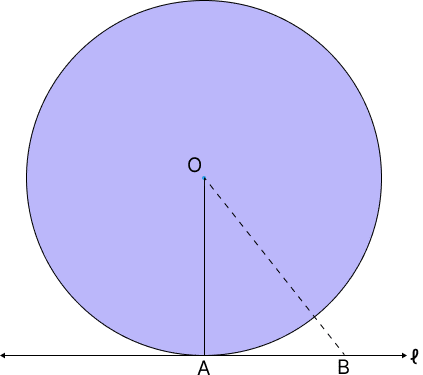
Explanation:
চিত্র অনুযায়ী,
ধরি O বৃত্তের কেন্দ্র এবং A বৃত্তের পরিধির উপর একটি বিন্দু।
A বিন্দুতে অঙ্কিত স্পর্শকটি হলো সরলরেখা ℓ
OA যোগ করি।
প্রমাণ করতে হবে—
\angle OAl = 90^\circ
ধরি,
ℓ রেখার উপর A ব্যতীত অন্য একটি বিন্দু হলো B
তাহলে B বিন্দু বৃত্তের বাইরে অবস্থিত।
অতএব,
কারণ OA হলো ব্যাসার্ধ এবং OB হলো কেন্দ্র থেকে বৃত্তের বাইরে অবস্থিত একটি বিন্দু পর্যন্ত দূরত্ব।
সুতরাং,
O থেকে ℓ রেখার উপর অঙ্কিত সকল রেখাংশের মধ্যে OA সর্বনিম্ন।
জ্যামিতির সূত্র অনুযায়ী,
কোনো বিন্দু থেকে সরলরেখার উপর অঙ্কিত সর্বনিম্ন দূরত্বটি লম্ব হয়।
অতএব,
OA \perp l
সুতরাং,
বৃত্তের কোনো বিন্দুতে অঙ্কিত স্পর্শক ও স্পর্শবিন্দুগামী ব্যাসার্ধ পরস্পর লম্বভাবে অবস্থিত।
প্রমাণিত।
10. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) একটি বৃত্তস্থ চতুর্ভুজ ABCD অঙ্কন করা হলো। বর্ধিত AB ও DC বাহুদ্বয় পরস্পরকে P বিন্দুতে ছেদ করলে প্রমাণ কর যে — PA \cdot PB = PC \cdot PD
Answer:
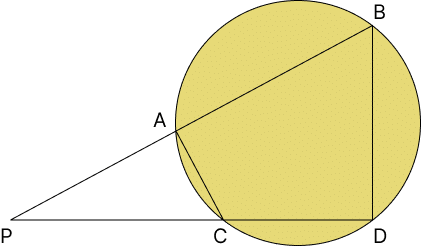
Explanation:
চিত্র অনুযায়ী,
AB ও DC বর্ধিত করলে তারা বৃত্তের বাইরে P বিন্দুতে ছেদ করে।
যোগ করি—
PA, PB, PC এবং PD।
বিবেচনা করি △PAC এবং △PDB।
ত্রিভুজ দুটি থেকে পাই—
\angle PAC = \angle PDBকারণ,
এই দুটি কোণ একই বৃত্তস্থ খণ্ডের উপর অবস্থিত।
আবার,
\angle PCA = \angle PBDকারণ,
এই কোণ দুটিও একই বৃত্তস্থ খণ্ডের উপর অবস্থিত।
অতএব,
△PAC ∼ △PDB
সদৃশ ত্রিভুজের অনুপাত অনুযায়ী—
\frac{PA}{PD} = \frac{PC}{PB}উভয় পাশে
PB \cdot PD
দ্বারা গুণ করলে পাই—
অতএব,
PA \cdot PB = PC \cdot PD
প্রমাণিত।
(ii) △ABC এর ∠A সমকোণ। BP এবং CQ দুটি মধ্যমা হলে প্রমাণ কর যে — 5BC^2 = 4(BP^2 + CQ^2)
Answer:
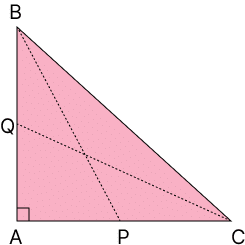
Explanation:
চিত্র অনুযায়ী,
△ABC একটি সমকোণী ত্রিভুজ যেখানে — ∠A = 90°
ধরি,
BC = অতিভুজ
P হলো AC-এর মধ্যবিন্দু
Q হলো AB-এর মধ্যবিন্দু
অতএব,
BP ও CQ হলো মধ্যমা।
আমরা জানি, যেকোনো ত্রিভুজে মধ্যমার দৈর্ঘ্যের সূত্র—
এখন দুটি যোগ করি —
BP^2 + CQ^2 = \frac{1}{4}(2BA^2 + 2CA^2 + 4BC^2 - AC^2 - AB^2)
সরল করলে পাই —
= \frac{1}{4}(BA^2 + CA^2 + 4BC^2)যেহেতু ∠A = 90°,
পাইথাগোরাস সূত্র অনুযায়ী—
অতএব,
BP^2 + CQ^2 = \frac{1}{4}(BC^2 + 4BC^2)
উভয় পাশে 4 দ্বারা গুণ করলে পাই—
4(BP^2 + CQ^2) = 5BC^2অতএব, 5BC^2 = 4(BP^2 + CQ^2)
প্রমাণিত।
11. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) 4 সেমি ও 3 সেমি দৈর্ঘ্য বিশিষ্ট রেখাংশের মধ্যমানুপাতি নির্ণয় করো।
Answer: 2\sqrt{3} সেমি
Explanation:
ধরি,
4 সেমি ও 3 সেমি দৈর্ঘ্য বিশিষ্ট রেখাংশের মধ্যমানুপাতি = x
মধ্যমানুপাতির সংজ্ঞা অনুযায়ী—
4 : x = x : 3অতএব,
x^2 = 4 \times 3
x^2 = 12
x = \sqrt{12}
x = 2\sqrt{3}
সুতরাং,
মধ্যমানুপাতি = 2\sqrt{3} সেমি
12. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ
(i) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 42 সেমি। এই বৃত্তে 11 সেমি দৈর্ঘ্যের বৃত্তচাপ দ্বারা গঠিত কেন্দ্রীয় কোণটির বৃত্তীয় মান নির্ণয় করো।
Answer: \frac{\pi}{12}
Explanation:
ধরি,
বৃত্তের ব্যাসার্ধ r = 42 সেমি
বৃত্তচাপের দৈর্ঘ্য s = 11 সেমি
আমরা জানি, বৃত্তচাপের দৈর্ঘ্য এবং কেন্দ্রীয় কোণের মধ্যে সম্পর্ক হলো—
s = r\theta (যেখানে \theta কোণটি রেডিয়ান বা বৃত্তীয় এককে থাকে)
সুতরাং,
\theta = \frac{s}{r}
মান বসিয়ে পাই—
\theta = \frac{11}{42} রেডিয়ান
এখন উত্তরটিকে \pi-এর মাধ্যমে প্রকাশ করার জন্য লব ও হরকে 2 দিয়ে গুণ করি:
\theta = \frac{11 \times 2}{42 \times 2} = \frac{22}{84}
যেহেতু \pi \approx \frac{22}{7}, তাই আমরা লিখতে পারি 22 = 7\pi। মানটি বসিয়ে পাই—
\theta = \frac{7\pi}{84}
লঘিষ্ঠ করলে পাই—
\theta = \frac{\pi}{12}
সুতরাং, কেন্দ্রীয় কোণটির বৃত্তীয় মান = \frac{\pi}{12}
(ii) \cot^4\theta - \cot^2\theta = 1 হলে দেখাও যে \sec^4\theta - \sec^2\theta = 1
Answer:
\sec^4\theta - \sec^2\theta = 1
Explanation:
দেওয়া আছে — \cot^4\theta - \cot^2\theta = 1
ধরি, \cot^2\theta = x
তাহলে সমীকরণটি হবে — x^2 - x = 1
অথবা, x^2 - x - 1 = 0
এখন আমরা জানি — \sec^2\theta = 1 + \tan^2\theta
এবং, \tan^2\theta = \frac{1}{\cot^2\theta} = \frac{1}{x}
অতএব, \sec^2\theta = 1 + \frac{1}{x} = \frac{x+1}{x}
এখন,
\sec^4\theta - \sec^2\theta
= \left(\frac{x+1}{x}\right)^2 - \frac{x+1}{x}
= \frac{(x+1)^2 - x(x+1)}{x^2}
= \frac{x^2 + 2x + 1 - x^2 - x}{x^2}
= \frac{x+1}{x^2}
এখন,
x^2 - x - 1 = 0
থেকে পাই — x^2 = x + 1
অতএব,
\frac{x+1}{x^2} = 1
সুতরাং,
\sec^4\theta - \sec^2\theta = 1
প্রমাণিত।
(iii) সমাধান করো x^2 - \sin^2\frac{5\pi}{18} - \sin^2\frac{2\pi}{9} = 0
Answer:
x = \pm 1
Explanation:
প্রথমে কোণগুলো ডিগ্রিতে রূপান্তর করি—
\frac{5\pi}{18} = 50^\circ
\frac{2\pi}{9} = 40^\circ
তাহলে সমীকরণটি হবে—
x^2 - \sin^2 50^\circ - \sin^2 40^\circ = 0
এখন উভয় পাশে
\sin^2 50^\circ এবং
\sin^2 40^\circ
যোগ করি—
যেহেতু
50^\circ + 40^\circ = 90^\circ
অতএব,
\sin 40^\circ = \cos 50^\circ
সুতরাং,
\sin^2 50^\circ + \sin^2 40^\circ = \sin^2 50^\circ + \cos^2 50^\circ
পিথাগোরাসের ত্রিকোণমিতিক অভেদ অনুযায়ী—
\sin^2\theta + \cos^2\theta = 1অতএব, x^2 = 1
সুতরাং, x = \pm 1
(i) দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটার ও 60 মিটার। প্রথমটির গোড়া থেকে দ্বিতীয়টির গোড়ার উন্নতি কোণ 30° হলে, দ্বিতীয়টির গোড়া থেকে প্রথমটির চূড়ার উন্নতি কোণ কত?
Answer: 60^\circ
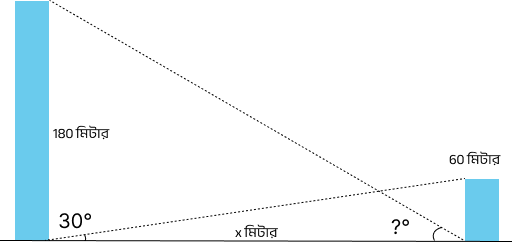
Explanation:
ধরি,
প্রথম স্তম্ভের উচ্চতা = 180 মিটার
দ্বিতীয় স্তম্ভের উচ্চতা = 60 মিটার
দুটি স্তম্ভের গোড়ার মধ্যবর্তী অনুভূমিক দূরত্ব = x মিটার
প্রথম স্তম্ভের গোড়া থেকে দ্বিতীয় স্তম্ভের গোড়ার দিকে তাকালে
উন্নতি কোণ = 30^\circ
অতএব, সমকোণী ত্রিভুজ থেকে—
\tan 30^\circ = \frac{180-60}{x} \tan 30^\circ = \frac{120}{x} \frac{1}{\sqrt{3}} = \frac{120}{x} x = 120\sqrt{3}এখন দ্বিতীয় স্তম্ভের গোড়া থেকে প্রথম স্তম্ভের চূড়ার উন্নতি কোণ ধরি \theta।
তাহলে—
\tan \theta = \frac{180}{120\sqrt{3}} \tan \theta = \frac{3}{2\sqrt{3}} \tan \theta = \frac{\sqrt{3}}{2}এখন আমরা জানি —
\tan 60^\circ = \sqrt{3}
এবং \tan 30^\circ = \frac{1}{\sqrt{3}}
সুতরাং, \theta = 60^\circ
অতএব, দ্বিতীয় স্তম্ভের গোড়া থেকে প্রথমটির চূড়ার উন্নতি কোণ = 60°
সমাধান সহ PDF টি 2nd February 2026 এর আগে Publish করা হবে।





